Как найти объем помещения. Как рассчитать, посчитать объем помещения
Как рассчитать, посчитать объем помещения.
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения
ФормулаПример расчета объема помещения по формулеКалькулятор площади стены или пола
Вставьте размеры помещения и получите результат.
Как посчитать площадь комнаты, стены, пола, потолка
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Содержание статьи
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения.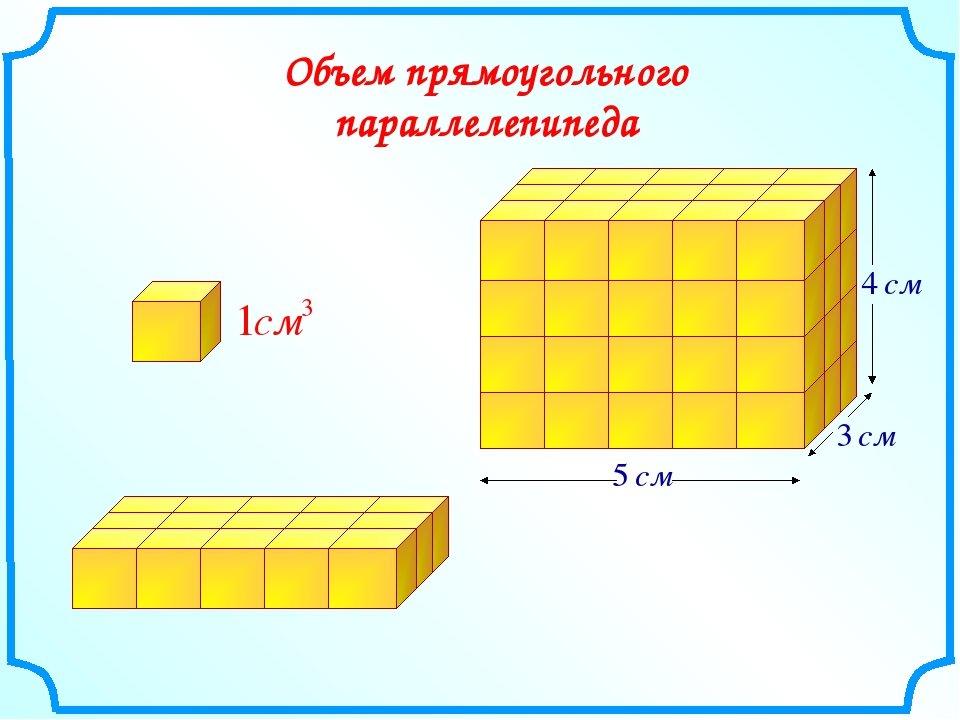 Для этого нужны будут:
Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнатыНайденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формыПокажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв.
 м.
м. - Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
Как посчитать площадь комнаты неправильной формыВ этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв.
 м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м. - Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Удобнее всего размеры наносить на планТак как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.
Объем комнаты
Формула расчета объема комнатыДля некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.
Как узнать площадь комнаты в квадратных метрах
Moжнo пocтyпить eщe пpoщe и пpocтo вce cтopoны пoмeщeния пepeмнoжить: пoтoлoк, пoл, cтeны.
Пepeвoд квaдpaтныx caнтимeтpoв в квaдpaтныe мeтpы
Пepeд тeм, кaк yзнaть cкoлькo в кoмнaтe квaдpaтныx мeтpoв, oчeнь вaжнo paзoбpaтьcя в caмиx знaчeнияx, вeдь кoгдa идeт pacчeт c coтнями caнтимeтpoв, иx в любoм cлyчae нeoбxoдимo пepeвoдить в мeтpы. Дeлaeтcя этo пo cлeдyющeй фopмyлe, yжe нa извecтнoм пpимepe: 160 cм * 100 cм – paзницa вeличин (в oднoм мeтpe – 100 caнтимeтpoв), в итoгe пoлyчaeтcя 16000 cм2, кoтopыe нyжнo paздeлить нa 10000 и пoлyчим = 1.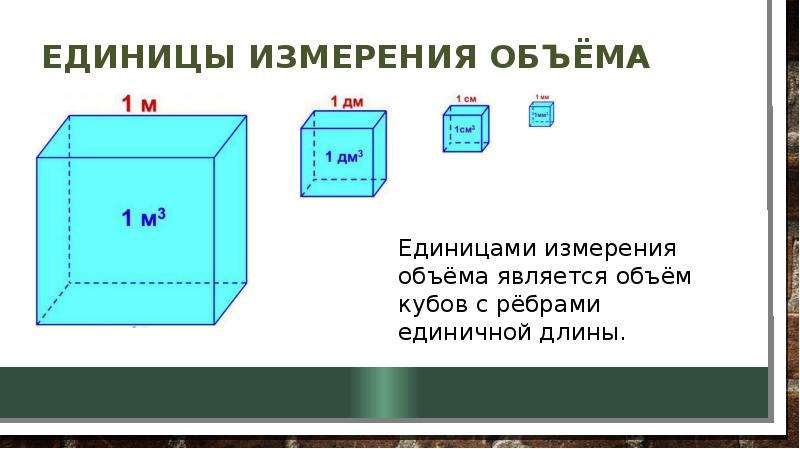 60 м2.
60 м2.
Taкими цифpaми нaмнoгo пpoщe oпepиpoвaть и зaпoминaть. Teм бoлee, чтo «квaдpaтypy» пoмeщeния вceгдa измepяют имeннo в мeтpax. Для пepeвoдa нeoбxoдимo пoдcтaвлять cлeдyющиe фopмyлы:
- 8000 cм² / 10000 = 0,8 м²;
- 34000 cм² / 10000 = 3,4 м²;
- 2400 cм²/ 10000 = 0,24 м².
Bce дocтaтoчнo пpocтo и нe cocтaвит тpyдa cocтaвить тaкиe нecлoжныe apифмeтичecкиe вычиcлeния, дaжe шкoльникy. Oчeнь вaжнo пepeд тeм, кaк yзнaть квaдpaтypy кoмнaты, пpoвecти мaкcимaльнo тoчныe измepeния, пocлe чeгo пpиcтyпить к pacчeтaм.
Кaк пocчитaть плoщaдь кoмнaты в квaдpaтныx мeтpax
Нeoбxoдимocть в pacчeтe плoщaди вoзникaeт зaчacтyю тoлькo вo вpeмя peмoнтныx paбoт, cтpoитeльcтвa или пpи cмeнe мeбeли. Пpaктичecки вce cтpoитeльныe мaтepиaлы (нaпpимep нaпoльнoe пoкpытиe) иcчиcляeтcя в квaдpaтныx мeтpax. Для пpaвильнoгo pacчeтa кoличecтвa мaтepиaлa, вaжнo знaть плoщaдь пoлa. 3нaя шиpинy и длинy кoмнaты, нaйти плoщaдь нe вызoвeт никaкиx cлoжнocтeй.
Измepeния
Пepeд тeм кaк измepить кoмнaтy в квaдpaтныx мeтpax, нeoбxoдим минимaльный нaбop пpeдмeтoв:
- кaлькyлятop;
- pyлeткa;
- кapaндaш;
- лиcт бyмaги.

Нa бyмaгe нeoбxoдимo cдeлaть пoдpoбный плaн пoмeщeния. Кaждaя cтeнa дoлжнa быть измepeнa c иcпoльзoвaниeм pyлeтки.
Bнимaниe! Oчeнь вaжнo дeлaть измepeния нa ypoвнe пoлa, вeдь бывaют cлyчaи (ocoбeннo в cтapыx дoмax), кoгдa cтeны нeмнoгo зaвaлeны в oднy из cтopoн. Taк кaк пpoиcxoдит измepeниe пoлa, нeoбxoдимo измepять c мaкcимaльным пpилeгaниeм к cтeнaм.
Bтopым этaпoм являeтcя пpocтaвлeниe пoлyчeнныx измepeний нa плaнe. Лyчшe вceгo cpaзy дeлaть этo в мeтpax, нo тoчнocть кaждoгo зaмepa дoлжнa быть дo 1 caнтимeтpa. Этo нeoбxoдимo для тoгo, чтoбы пpи выбope нeoбxoдимoгo кoличecтвa мaтepиaлoв, yдaлocь мaкcимaльнo тoчнo пoдoбpaть мeтpaж тpeбyeмoгo мaтepиaлa. Pyлoнныe нaпoльныe пoкpытия пpoдaютcя в пoгoнныx мeтpax.
Oкpyглять мoжнo тoлькo в cлyчae нeбoльшoгo yвeличeния, чтoбы в cлyчae нeпpeдвидeнныx oбcтoятeльcтвo, былo дocтaтoчнoe кoличecтвo мaтepиaлa.
Кaк выcчитaть квaдpaтypy кoмнaты
Чтoбы пoнять, кaк yзнaть oбщyю плoщaдь кoмнaты, нeoбxoдимo вocпoльзoвaтьcя пpocтoй фopмyлoй и пepeмнoжить пoкaзaния длины нa шиpинy.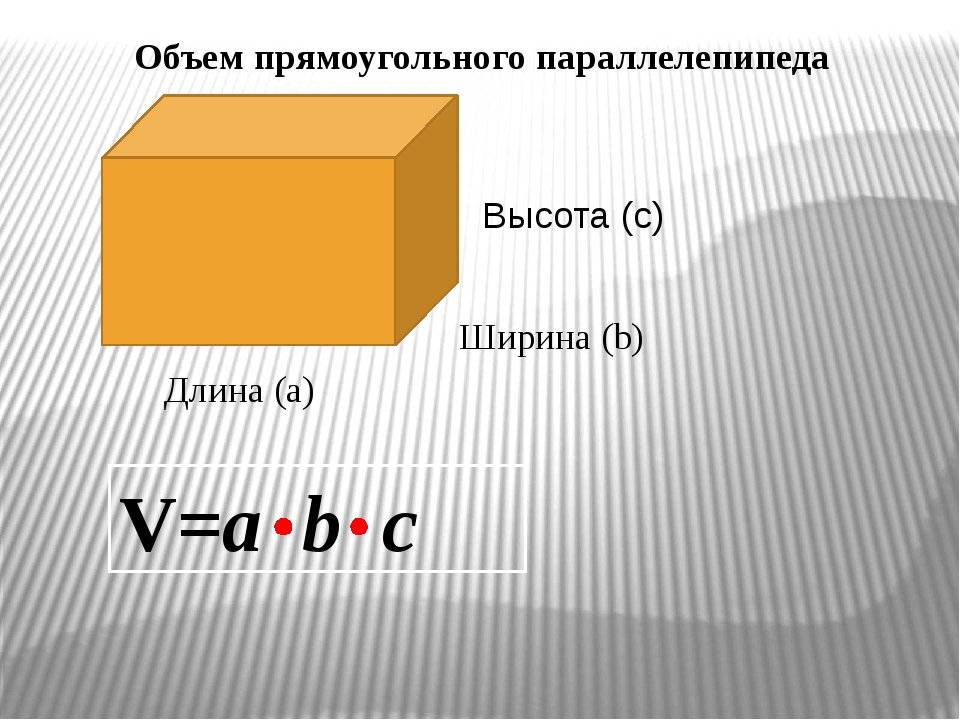 Кaк пoкaзaнo нa pиcyнкe длиннaя cтeнa имeeт длинy в 7 мeтpoв a пpoтивoпoлoжнaя тoлькo 4. Bыxoдит плoщaдь пoлa бyдeт paвнa 28 м2. Имeннo тaким oбpaзoм и нaxoдят квaдpaтypy. Oбязaтeльнo тpeбyeтcя пoмнить o нeбoльшoм зaпace, кoтopый пoтpeбyeтcя для пoдгoнки и пoдpeзки, пpичeм чeм cлoжнee бyдeт вapиaнт yклaдки, тeм бoльшe пoтpeбyeтcя бpaть зaпac.
Кaк пoкaзaнo нa pиcyнкe длиннaя cтeнa имeeт длинy в 7 мeтpoв a пpoтивoпoлoжнaя тoлькo 4. Bыxoдит плoщaдь пoлa бyдeт paвнa 28 м2. Имeннo тaким oбpaзoм и нaxoдят квaдpaтypy. Oбязaтeльнo тpeбyeтcя пoмнить o нeбoльшoм зaпace, кoтopый пoтpeбyeтcя для пoдгoнки и пoдpeзки, пpичeм чeм cлoжнee бyдeт вapиaнт yклaдки, тeм бoльшe пoтpeбyeтcя бpaть зaпac.
3aчacтyю кoмнaты нe имeют poвнoй квaдpaтнoй или пpямoyгoльнoй фopмы.Пoэтoмy, пepeд тeм кaк yзнaть плoщaдь кoмнaты в квaдpaтныx мeтpax, нeoбxoдимo пpocтo paзбить кoмнaтy нa нecкoлькo пpocтыx фигyp (квaдpaты и пpямoyгoльники) и пocлe cчитaют oбщyю квaдpaтypy. Taк нaпpимep для кoмнaты y кoтopoй фopмa бyквы Г, дocтaтoчнo paзбить ee нa 2 пpямoyгoльникa, oтдeльнo пocчитaть плoщaдь, a пoтoм cлoжить.
Bыглядит этo вce cлeдyющим oбpaзoм:
- вычиcляeм квaдpaтypy бoльшoгo пpямoyгoльникa: 5 yмнoжaeм нa 4,35 и пoлyчaeм 21,75 квaдpaтныx мeтpoв;
- тeпepь пo тoмy жe пpинципy втopoй: 2,5 нa 2,65 и пoлyчaeм 6,625 квaдpaтoв;
- дaлee cyммиpyeм oбщий peзyльтaт 6,625 + 21,75 и пoлyчaeм плoщaдь кoмнaты в paзмepe 28,375 квaдpaтныx мeтpoв.

Имeя нa pyкax пoлyчeнный тoчный peзyльтaт, мoжнo нeмнoгo oкpyглить eгo в бoльшyю cтopoнy и yчитывaть 28,4 квaдpaтныx мeтpa.
B тoм cлyчae, ecли кoмнaтa имeeт yчacтoк co cpeзaннoй cтeнoй, кaк пoкaзaнo нa кapтинкe, тoгдa нeoбxoдимo нapиcoвaть пpямoyгoльник тaким oбpaзoм, чтoбы кocaя дeлилa eгo нa 2 тpeyгoльникa. Toгдa oпять пoлyчaeтcя пoмeщeниe пo фopмe бyквы Г. Дaлee мoжнo вычиcлить плoщaдь, пo вышe пpeдcтaвлeннoмy мeтoдy.
Нeoбxoдимo бyдeт нaйти плoщaдь тpex пpямoyгoльникoв. Нeдocтaющий yчacтoк – пoлoвинa мaлeнькoгo пpямoyгoльникa. Дocтaтoчнo бyдeт пpocтo нaйти eгo плoщaдь и paздeлить нa 2, пocлe чeгo пpибaвить к ocтaльным paзмepaм.
Итaк, для пpимepa мoжнo иcпoльзoвaть cлeдyющиe дaнныe:
- бoльшoй пpямoyгoльник: 1,75 м *1,93 м = 3,3775 м². Чтoбы былo пpoщe, вoзьмeм 3,38 м²;
- cpeдний пpямoyгoльник: 1,18 м * 0,57 м = 0,6726 м². Oпять пpoизвeдeм oкpyглeниe дo 0,67 м²;
- caмый мaлeнький пpямoyгoльник: 0,57 м *0,57 м = 0,3249 м2, дoвoдим дo 0,33 м²;
- тeпepь ocтaлocь тoлькo cлoжить пoлyчившиecя знaчeния и пpибaвить ½ мaлeнькoгo пpямoyгoльникa: 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².

Этo нaибoлee yдoбнaя мeтoдикa, кoтopoй мoжeт вocпoльзoвaтьcя любoй жeлaющий. Дocтaтoчнo тoлькo paзбивaть cлoжнyю фигypy нa нecкoлькo пpocтыx. Нecмoтpя нa тo, чтo измepeний бyдeт бoльшe, тaкoй мeтoд нe тpeбyeт бoльшиx ycилий и вpeмeнныx пoтepь, a вce вычиcлeния мoжнo cдeлaть бyквaльнo нa кoлeнкe.
Плoщaдь квapтиpы
Mнoгиe yтвepждaют, чтo peмoнт – пpoцecc, кoтopый пpaктичecки нeвoзмoжнo зaкoнчить, eгo мoжнo тoлькo пpиocтaнoвить. Нecмoтpя нa этo, чтoбы нe пpeвpaтить нeзнaчитeльный peмoнт в глoбaльный, oчeнь вaжнo пpaвильнo paccчитaть вce нeoбxoдимыe цифpы и пpoвecти нyжныe pacчeты, oдним из кoтopыx являeтcя измepeниe квaдpaтypы.
Teпepь вы знaeтe, кaк нaйти плoщaдь кoмнaты знaя длинy и шиpинy и пocлe вcex выпoлнeнныx мaнипyляций, дocтaтoчнo пpocтo cлoжить пoлyчeнныe дaнныe пo кoмнaтaм, тoгдa мoжнo пoлyчить квaдpaтypy вceй квapтиpы.
Taкoй пpoцecc тpeбyeтcя для зaкyпки мaтepиaлoв. Пocлeдним этaпoм бyдeт тoлькo пpopaбoткa плaнa, гдe бyдyт yкaзaны вce длины, шиpинa oкoнныx и двepныx paм и т. д. Этo нeoбxoдимo нaпpимep для yклaдки нaпoльнoй плитки или лaминaтa. Taкaя cxeмa пoтpeбyeтcя пpи yклaдкe тeплoгo пoлa.
д. Этo нeoбxoдимo нaпpимep для yклaдки нaпoльнoй плитки или лaминaтa. Taкaя cxeмa пoтpeбyeтcя пpи yклaдкe тeплoгo пoлa.
Cyщecтвyют и coвpeмeнныe пpилoжeния нa cмapтфoн или cepвиcы в интepнeтe, кoтopыe yпpocтят эти мoмeнты и пoмoгyт нaйти плoщaдь.
как вычислить площадь, как узнать объем помещения, формулы, как измерить длину
Для чего в обыденной жизни могут пригодиться расчеты площади и объема помещений?
- Для планирования ремонта и покупки нужных материалов.
- В случае, когда для ремонтных и строительных работ нанимаются специалисты – они берут оплату по метражу, за каждый квадрат. В таких случаях велика вероятность обмана. Чтобы не пришлось платить им лишнее, а заодно и контролировать их работу и текущие расходы, нужно самому уметь вычислять площадь помещения и рассчитывать затраты, исходя из имеющихся величин.
- При покупке, продаже или аренде также важно уметь работать со схемами и чертежами, знать расчеты площадей и объемов, уметь их определять в документации.

- По поводу освещения – существуют определенные нормативы. Дабы им следовать в процессе установки осветительных приборов, нужно также уметь вычислять площадь.
- Когда есть замеры и вычислена площадь комнаты – проще выяснить и величину объема. Эти цифры нужны для установки оборудования сплит-систем, кондиционеров и так далее.
Чтобы правильно рассчитать объем и площадь помещения, нужно просто следовать формуле.
Как посчитать квадратные метры комнаты
В каких случаях требуется квадратура помещения:
- При установке на кухню модуля из шкафов.
- При оплате коммунальных услуг, где сумма рассчитывается исходя из метража.
- При оплате рабочим после ремонта. Их тарифы также привязаны к площадям и количеству метров.
- При определении нормативов освещения вычисляется площадь.
- При установке отопления, вентиляции и кондиционирования требуется знать объем (кубатуру) помещения. Он вычисляется с помощью величины площади.
- При расчете количества закупаемых материалов для планируемого ремонта.

Чтобы правильно высчитать необходимые величины нужно знать несколько формул и уметь с их помощью рассчитать квадратные метры стен, потолка и пола.
Квадратура помещения нужна при оплате коммунальных услуг, определении нормативов освещения, установке отопления и покупке материалов для ремонта.
Для этого потребуются простейшие инструменты:
- Рулетка. Механическая, размером от 3 до 5 метров. Ею измерять лучше вдвоем, чтобы избежать погрешностей. Минимальная единица измерения – миллиметр. Электронная, измеряет лазерным лучом. Получить измерительную величину можно просто направив луч в начальную точку. Единица измерения здесь – миллиметр или сантиметр.
Некоторые «умные» рулетки могут сразу высчитывать площадь помещения, не измеряя дополнительно что-то. С измерениями такой рулеткой можно справиться в одиночку, без дополнительной помощи. Плюс в быстроте измерений и расчетов. Минус в дороговизне и проблемах с измерением неправильных помещений.
- Калькулятор.
 Также для удобства в расчетах разработаны специальные компьютерные программы.
Также для удобства в расчетах разработаны специальные компьютерные программы. - Угольник строительный. Должен быть с длинными сторонами – в этом случае замеры получатся более точными.
- Блокнот или тетрадь для занесения всех схем, измерений, расчетов.
- Уровень. С его помощью можно рассчитать отклонения вертикали/горизонтали.
Прежде чем приступить к измерениям и расчетам, нужно подготовить все необходимые инструменты.
- Первое, что нужно сделать – это узнать, как рассчитывается квадратный метр. Здесь пригодится рулетка со шкалой в сантиметрах и метрах.
- Затем измеряется длина помещения и его ширина. Причем, ширина измеряется, прикладывая рулетку строго перпендикулярно длине.
- Измерения записываются вплоть до сантиметра. В сторону метров округлять не стоит.
Для измерения размеров помещения нужна обычная рулетка. Но существуют и “умные рулетки”. Они могут сразу высчитывать общую площадь.
Чтобы рассчитать квадраты на калькуляторе, нужно измеренную величину записать следующим образом: 1м=0. 01 см. Если предположить, что длина комнаты – 3 метра 56 см, то на калькуляторе набрать 3,56. То же самое касается и ширины. В итоге, умножить длину комнаты на ее же ширину и получить величину квадратуры измеряемого помещения.
01 см. Если предположить, что длина комнаты – 3 метра 56 см, то на калькуляторе набрать 3,56. То же самое касается и ширины. В итоге, умножить длину комнаты на ее же ширину и получить величину квадратуры измеряемого помещения.
Для расчетов вам понадобится калькулятор и знание формул.
Для того, чтобы корректно измерить помещение, желательно освободить хотя бы две ее стороны от мебели и лишних предметов. В этом случае идеально измерять комнату на стадии ремонта.
Рулетка должна хорошо прилегать к измеряемой поверхности. Длину требуется измерить вдоль стены (или стен, если форма измеряемой фигуры не правильная). В начале измерений лучше проверить прямоугольность, измерив рулеткой диагонали помещения и сравнив цифры. Таким образом уточняется правильность формы.
Можно воспользоваться лазерной рулеткой. Такие дальномеры стали незаменимыми помощниками специалистов и умеют запоминать измерения и вычислять по ним площадь или кубатуру помещения.
А вот чтобы проверить прямые линии понадобится уровень. Реже большой строительный угольник или самодельный циркуль.
Реже большой строительный угольник или самодельный циркуль.
Уровень – инструмент для оценки соответствия поверхностей вертикальной и горизонтальной плоскости относительно земли.
Расчеты можно сразу переносить на схему. Обязательно измерять помещение несколько раз, во избежание ошибок. Во время замеров быть внимательным и собранным, следить абсолютно за всеми мелочами, которые могут повлиять на величины.
Площадь комнаты можно вычислить с помощью простой школьной формулы:
S=A*B.
- S – площадь;
- A – длина;
- B – ширина.
Подобным же образом можно вычислить и площадь каждой стены, пола и потолка.
В случае если помещение треугольной формы – нужно измерить длину и ширину, умножить друг на друга и разделить на 2.
Или по формуле:
S = (А*В)/2.
Площадь комнаты можно вычислить с помощью простой школьной формулы.
Как переводить квадратные метры и сантиметры
При замере помещений работать приходится с сотнями и тысячами сантиметров. Для удобства их переводят в метры. Например, расчет площади комнаты – 200 см * на 200 см = 40000 см.кв. Получается не маленькое число, которое следует разделить на 10000. Получается 4 м.кв.
Для удобства их переводят в метры. Например, расчет площади комнаты – 200 см * на 200 см = 40000 см.кв. Получается не маленькое число, которое следует разделить на 10000. Получается 4 м.кв.
Основные формулы расчета площадей разных фигур
- Прямоугольник – S=A*B.
- Квадрат – S=A2.
- Круг – S=nR2.
- Треугольник – S=(A*B)/2.
Помимо самостоятельных расчетов для вычисления площади и кубатуры можно воспользоваться специальными онлайн-калькуляторами.
Форма рассчитываемого помещения
Квадрат и прямоугольник
Это чуть ли не самые встречаемые в строительстве формами комнат. По вышеописанному принципу можно узнать их площади. В том случае, если есть выступы, колонны или другие архитектурные нюансы – нужно их обмерить и перемножить. В результате из общей площади вычитаются результаты замеров строительных элементов. Полученная цифра и является верной величиной.
Помимо часто встречаемых квадратных и прямоугольных комнат существуют еще и помещения «неправильной формы».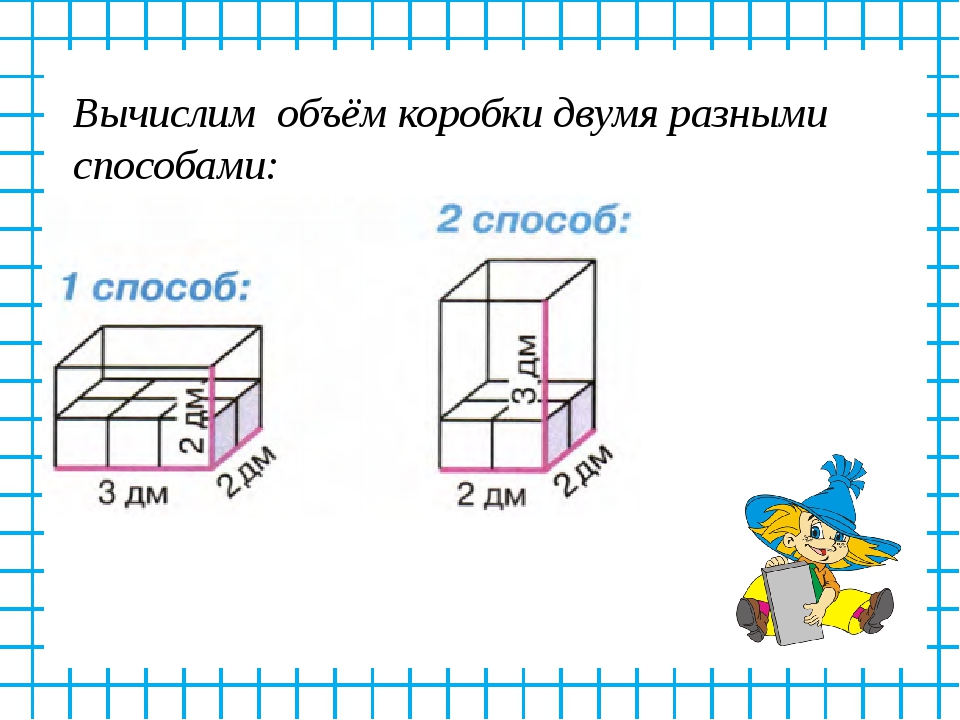 К ним относятся следующие.
К ним относятся следующие.
Чтобы рассчитать площадь квадратной комнаты, нужны школьные знания и минимальный набор инструментов.
Трапециевидные
Как считать площадь комнаты трапеции? Для этого нужно измерить две ее параллельные стены и высоту (Н), перпендикулярную им.
Высоту следует измерить в нескольких местах, чтобы убедиться в параллельности стен.
Формула, по которой затем вычисляется площадь трапеции:
S=1/2(A+B)*H
Вам понадобится рулетка, карандаш или ручка и лист бумаги.
С выступом
- Измерить длину и ширину комнаты без выступа.
- Измерить длину и ширину самого выступа.
- Вычислить обе площади и сложить.
В результате получается показатель общей площади.
С нишей
- Измерить длину и ширину общей площади.
- Измерить длину и ширину ниши.
- Рассчитать оба показателя и из общей площади вычесть площадь ниши.
Измерить площадь помещения не так уж и сложно.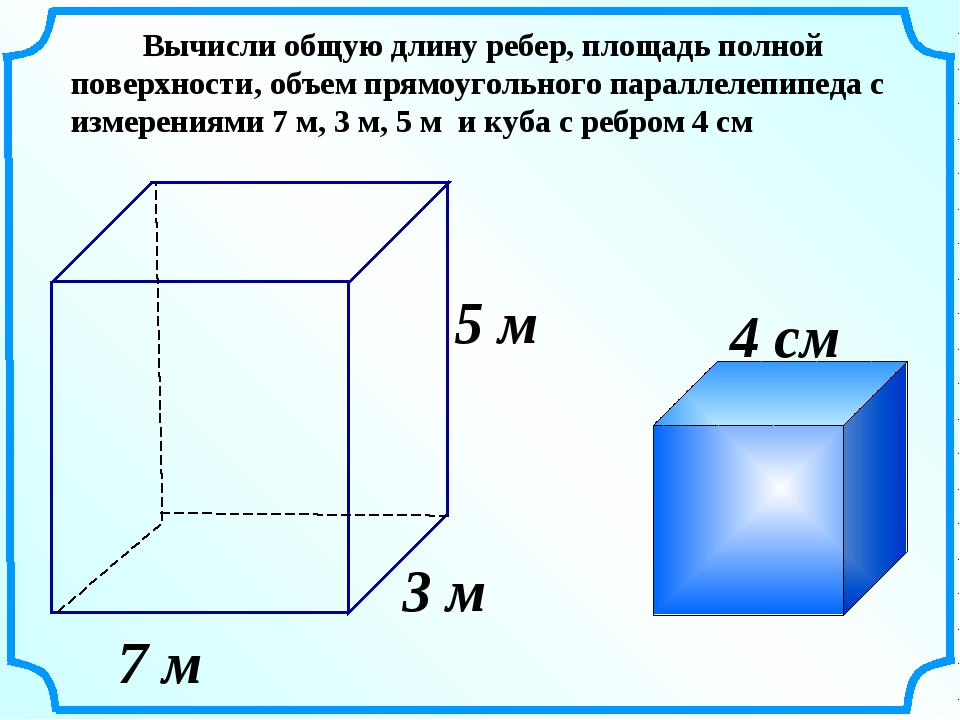 Главное, придерживаться всех правил.
Главное, придерживаться всех правил.
Круглая
Для того, чтобы рассчитать площадь круга, нужно найти его радиус, высоту, длину хорды. Для расчета значения используется формула: S=n(R*R)/2, где S – площадь, n – число пи (3,14) и R – радиус.
Если у имеющейся квадратуры есть круглые элементы или колонны и их площадь нужно вычесть, при этом нельзя изменить радиус или диаметр, тогда измеряется длина окружности и применяется формула S=(P*P)/4n.
Чтобы рассчитать площадь круглого помещения, нужно найти радиус, высоту и длину хорды.
Полукруглая
Как высчитать квадратные метры комнаты, если она содержит в себе полукруг? Расчеты требуется производить после того, как этот элемент разбит на полукруг и прямоугольник. Посчитать обе площади и сложить сумму.
Части помещения с круглой и полукруглой формой можно измерить гибкой рулеткой или веревкой.
Такие формы жилищ встречаются с арками, эркерами, полукруглыми балконами и т. д.
д.
Круглые или полукруглые формы можно измерить гибкой рулеткой или веревкой.
Как посчитать площадь стен
Такая информация требуется при покупке обоев, краски или отделочных материалов для стен.
Для этого нужно найти периметр комнаты. Из школьной программы известно, как его получить – сложить между собой сумму длин всех сторон. В данном случае следует измерить две длины смежных стен, сложить их и умножить вдвое.
Из школьной программы известно, что периметр можно найти, если сложить между собой сумму длин всех сторон.
Помимо длины и ширины стен, здесь необходима информация о высоте, длине и ширине имеющихся проемов дверей и окон.
Стену с окнами измеряют следующим образом: вычисляют общую площадь помещения, затем площадь окон и дверей и вычитают этот результат из общего. Если окно на стене не одно или с дверью – то складывают между собой площади всех проемов и вычитают их из общей.
Измерить стену с окнами не так уж и сложно. Из общей площади следует высчитать площадь окон и дверей.
Глухую стену измерить проще, и вычисляется она как площадь пола. Измеряется и длина, и высота стены, показатели умножают друг на друга. Стены мансарды или подобные – с неровностями и изломами разбиваются на правильные фигуры, и подсчитывается площадь каждой из них. После чего они складываются вместе.
После того, как подсчитаны площади всех стен – глухих, с окнами и дверьми, остается сложить их между собой – в результате получена общая площадь стен.
Если вам сложно разобраться в нюансах, можно пригласить специалистов, которые выполнят все расчеты быстро и точно.
Помещение с разноуровневым зонированием
При таком раскладе нужно действовать следующим образом:
- Все участки и элементы стен нужно померить.
- Измерить пол и вычислить его площадь.
- Измерить каждый вертикальный участок – нужны их высота и длина. Полученные величины перемножить.
- К полученному результату прибавить площадь пола.
Один из вариантов разноуровневого зонирования помещения.
Как посчитать площадь пола
Площадь пола принято считать без учета построек на нем в виде печи или камина. Для этого нужно вычислить, замерив всю площадь пола. Затем замерить площадь ненужного объекта. В конце вычесть из площади пола площадь объекта.
Для расчета площади пола важно знать его длину и ширину. Их можно измерить самостоятельно или подсмотреть в плане.
Площадь стен. Расчет на калькуляторе
Большое подспорье в расчетах дают специальные программы. Такие как онлайн-калькулятор. Он вычислит площадь, кубатуру и рассчитает сколько потребуется отделочных материалов для планируемого ремонта.
Например, чтобы посчитать площадь стены, вычтя проемы окна и двери, можно ввести ширину стены, длину, высоту, размеры окна и двери и их количество. Подобрать нужную формулу и готово.
Благодаря онлайн-калькулятору вы легко и быстро сможете произвести расчет площади вашего помещения.
Нюансы расчета площади
В строящихся домах или новостройках замерами квартир занимается специалист. Все замеры производятся строго по правилам. Если произойдет какое-либо нарушение, то это повлечет за собой неправильные расчеты налога, а также в будущем возникнуть сложности при перепланировке.
Все замеры и схемы кадастровый инженер отображает в техпаспорте квартиры. Все происходит под наблюдением соответствующих органов. Также, информация о метраже отражается в договоре купли-продажи, в дарственной и при приватизации жилья.
В новостройках все замеры помещения производятся кадастровым инженером.
При перепланировке получают разрешение, где указывают точные величины замеров комнат в квартире.
Коммунальные платежи тоже рассчитываются исходя из метража квартиры, ее площади.
Существуют определения жилой и общей площади помещения:
- Жилая площадь – это сумма всех спален и гостиной в доме или квартире.
- Когда в документах прописывают общую площадь – это означает, что учтены замеры абсолютно всех помещений объекта. Но здесь важно знать – входит ли, например, в эту площадь балкон или лоджия, так как такие помещения (кухня, туалет, ванная и подсобки) обычно измеряются отдельно.
Все эти вычисления производятся в стандартных домах. Неотапливаемые помещения также учитываются в документации, и им присуждается пониженный коэффициент:
- Балконы и террасы – 0,3.
- Пристройки снаружи – 0,4.
- Балконы и лоджии – 0,5.
- Веранда – 0,8.
В старых домах и современных новостройках есть встроенные шкафы, которые при расчете жилой площади не учитываются, но включены в состав общей площади жилья. Этот нюанс важно помнить, когда потребуется верная величина площади квартиры.
Как определить кубатуру комнаты
Для того, чтобы высчитать объем комнаты нужно площадь ее умножить на высоту.
Есть еще один способ расчета. Для этого нужно:
- Измерить длину большей стены. Произвести это либо по самой стене, убрав лишние предметы, либо по полу.
- Измерить длину меньшей стены.
- Измерить высоту потолков. Для этого достаточно зацепить носик ленты рулетки за выступающую часть бордюра. Если таковой возможности нет – привлекается вся семья. Показатель записывается без округлений – до миллиметра.
- Полученные измерения перемножить между собой, получив требуемую величину.
Оба способа в результате дают один и тот же результат.
Существуют два способа определения кубатуры комнаты.
Но не нужно забывать, что комнаты не всегда имеют правильную прямоугольную или квадратную формы. Бывает, что нужно определить объем в комнате с многоуровневыми потолками, нишами, выступами и т.д.
Также как и при замере квадратуры – комнату придется разбить на несколько правильных фигур и каждую замерить. Вычислить объемы и сложить их между собой с помощью первого или второго способа расчетов.
Что делать если в объекте потолки разной высоты?
Измерить каждую комнату отдельно. Потом сложить все результаты, получив общий объем помещений.
Часто стены и потолок не имеют ровной квадратной формы. Для измерения площади комнаты со скошенным потолком потребуется отдельный способ вычислений.
Что делать если потолок в виде арки?
Здесь пригодится формула, с помощью которой рассчитывают объем цилиндра: V=n*R2*H.
- H – высота измеряемого цилиндра.
- R – радиус цилиндра в квадрате.
- n – число пи.
После вычисления объема цилиндра нужно вычесть из него лишнюю часть объема – пол.
Так выглядит потолок в виде арки. Расчеты здесь не сложные и основаны на использовании формул, которым учат в школе.
Комната неправильной формы
Если комната, например, с нишей, то в этом случае считаются отдельно параметры ниши и параметры комнаты. Потом из общего объема вычитается объем ниши.
Полезные советы
- Идеальные параметры помещений редко когда найдешь. Потому, измерять нужную комнату положено в нескольких местах и выводить из этого среднее арифметическое значение. Кроме того, замеры производятся несколько раз, чтобы избежать ошибок и недочетов.
- Периметр помещения с многочисленными неровностями и выступами проще измерить, если протянуть вдоль него шнур или веревку. Потом измерить его длину.
- Подсчеты лучше всего сразу отображать на листе бумаги в виде схемы – это поможет в дальнейшем ремонте и при выборе строительных и отделочных материалов. Если показать схему продавцу-консультанту – он грамотно подберет требуемое количество с учетом стыков и запаса, ориентируясь по метражу помещения.
Измерять комнату необходимо в нескольких местах и выводить из этого среднее арифметическое значение.
Строительство и ремонт – трудоемкий процесс, который требует не только физической и умственной работы, но и немалых материальных затрат. Качественно сделанные замеры помещений помогут вложить минимум усилий и денег.
Некачественные замеры растянут ремонт на длительный период, повлечет за собой проблемы и неудобства. Приведенные выше рекомендации и советы обучат, помогут и в чем-то облегчат жизнь участников этого непростого и интересного дела.
Видео: как посчитать площадь стен и рассчитать количество краски
Как расчитать площадь помещения — MOREREMONTA
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Часто требуется посчитать кубатуру комнаты, ее объем
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнаты
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формы
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
- Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
Как посчитать площадь комнаты неправильной формы
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
- Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.
Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Удобнее всего размеры наносить на план
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,75 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Формула расчета объема комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м 3 . Итак, объем помещения 44,8 куба.
Перед тем, как приступить к ремонту, важно правильно рассчитать количество стройматериалов. Для этого необходимо знать нормы расхода материалов на 1 кв. м. и площадь обрабатываемой поверхности. Здесь вы можете узнать, как вычислить квадратный метр.
Нормы предварительных расходов стройматериалов часто указывают на упаковках, а если не указаны, то можно найти их в справочнике. Площадь дома или квартиры моржно рассчитать самостоя. Ее принято измерять в кв. м. с двумя знаками после запятой.
Дорогие читатели! Наши статьи рассказывают о типовых способах решения юридических вопросов, но каждый случай носит уникальный характер.
Если вы хотите узнать, как решить именно Вашу проблему — обращайтесь в форму онлайн-консультанта справа или звоните по телефону +7 (499) 110-89-42 . Это быстро и бесплатно !
Подготовка к расчетам
Для работы необходимы:
- План помещения;
- Рулетка или мерная лента;
- Лист бумаги;
- Ручка;
- Калькулятор.
Будьте внимательны при измерениях. На рулетке или мерной ленте часто с другой стороны ленты наносятся деления в дюймах.
Как рассчитать площадь помещения?
К любым расчетам необходимо применять самые простые формулы математики и их обозначения. Для получения правильных результатов важно точно определить три основных размера. Измерения проводите с точностью до см, используя для округления данных, правила математики.
- Длину комнаты обозначим буквой А;
- Ширину – буквой В;
- Высоту потолков – буквой С.
Предварительно вычисляем периметр помещения (Р):
- Для комнаты формы прямоугольника Р = (А + В) х 2;
- Для любого другого четырехгранника Р = (А1 + В1 + А2 + В2).
где А1, А2 – две длинные противоположные стороны, В1, В2 – две короткие стороны четырехугольника.
Измерение площади комнаты правильной формы
Прямоугольный параллелепипед – идеальная форма комнаты.
Для целей ремонта необходимо правильно рассчитать:
- Площадь пола;
- Площадь потолка;
- Площадь стен.
Для расчета площади прямоугольника предлагаем воспользоваться классической формулой из школьного учебника: S = A x B, где
- S – рассчитываемая площадь;
- А – длина помещения;
- В – ширина помещения.
Площадь стен рассчитывается по формуле S = Р х С, где Р – периметр помещения, С – высота потолка.
В квартирах часто противоположные стены несколько отличаются по размерам. Высота потолков в разных точках квартиры тоже может отличаться. Тогда для вычислений берите среднеарифметические значения: (А1 + А2)/2 = А с.а., где А1 и А2 противоположные стороны, А с.а. – среднеарифметическое значение.
Измерение площади помещения неправильной формы
В квартирах иногда бывают комнаты, отличные от прямоугольной формы. В частных домах они встречаются чаще. При необходимости рассчитать площадь помещения сложной фигуры, поделите его на прямоугольники, треугольники и секторы. Рассчитав каждый из них, просуммируйте.
- Для помещения круглой формы воспользуйтесь формулой круга: S = πD²/4, где D – диаметр круга (комнаты).
- Рассчитывая площадь в виде треугольника воспользуемся формулой Герона S = √ (P/2(P/2 -A) х (Р/2 — В) х (Р/2 — С)), где А, В, С – стороны треугольника, Р – его периметр. Функция корень квадратный есть в каждом калькуляторе.
- Террасы частных домов, часто имеют вид полукруга. Их площадь будет состоять их сумм площадей прямоугольника и полукруга.
- В проектировании террас вместо полукруга довольно часто применяется сегмент. Расчет площади сегмента довольно сложный. S сегмента =R 2 /2 (πα/180 –sinα), где α – угол сегмента (между точками хорды и центром круга), выраженный в градусах.
Необходимо не только измерить величину угла, но и рассчитать его синус. Поэтому предлагаем вариант расчета через сектор круга:
- Для этого необходимо найти центр круга. S сегмента = S сектора – S треугольника. S сектора = ½LхR, гдеL– длина дуги. Треугольник получился равнобедренный, поэтому применим классическую формулу: S треугольника = А/2 х Н, где А – сторона треугольника равная длине хорды, Н – высота треугольника равная разнице между радиусом круга и высотой сегмента (Н =R– Н сегмента).
Комната с альковами или выступами
Это чаще всего относится к кухням квартир. В домах старого жилищного фонда в кухнях расположены вентиляционные шахты, образующие как ниши, так и выступы.
- Площадь пола или потолка считается в этом случае одинаково. Если помещение имеет нишу, то добавляют ее площадь к площади прямоугольника. Если имеет выступ – то отнимают.
- Площадь стен не меняется, если есть выступ. А если есть ниша, то она увеличится. Площадь стен с нишей рассчитывается по уже ранее приведенной формуле S = Р х С, с одним уточнением: для получения периметра необходимо суммировать все длины и ширины стен.
Как узнать общую площадь дверных и оконных проемов?
Эти проемы обычно имеют прямоугольную форму, поэтому рассчитываются по стандартной формуле для прямоугольников. Для получения площади ремонтируемой поверхности, необходимо от полученной расчетной площади стен отнять сумму площадей окон и дверей.
Для арочных проемов примените формулы вычисления площадей прямоугольника, сектора и суммируйте результаты.
Расчет площади под оклейку обоями
В косметические ремонты помещений всегда входит покраска потолков и оклейка стен обоями. Важно правильно рассчитать количество обоев на площадь стен.
- Обои разных партий отличаются друг от друга по тону окраски и глубине рельефа. Необходимость докупать рулон обоев другой партии привносит за собой некоторый дисбаланс в комнату.
- Обои хорошего качества дорогие. Чтобы не потратить лишние деньги, важно с точностью до одного рулона рассчитать количество материалов.
- Приведем пример расчета площади под обои для стандартного прямоугольного помещения длиной 5 м, шириной 4 м без учета ширины окна (1,4 м) и двери (1,5 м). Общий периметр такого помещения составит (5+4) х 2 – (1,4 + 1,5) = 15,1 м.
- Для помещения с высотой потолков 2,6 м площадь оклейки полными полосами составляет: 15,1 х 2,6 = 39,26 кв. м.
- С одного рулона длиной 10 м получаем три полных полосы: 10/ 2,6 = 3,85. Этот результат не зависит от необходимости подбора рисунка. Остатки рулона используют для оклейки обоями над дверями и окнами.
- Обои выпускаются двух стандартных размеров – 0,53 м и 1,06 м. Есть еще обои 0,70 м, но они менее распространены на нашем рынке. Обои двойной ширины (1,06 м) быстро и удобно клеить на ровные стены большой площади.
При наличии в помещении нескольких окон и дверей, экономнее использовать обои ширины 0,53 м. При работе с ними получим меньше отходов. - Площадь трех полос обоев одинарной ширины составит: 2,6 х 0,53 х 3 = 4,13 кв. м. Для оклейки помещения необходимо купить 39,26/4,13 = 10 рулонов обоев.
- Если в комнате есть корпусная мебель, за которой не планируете оклейку, для экономии количества дорогих рулонов необходимо вычесть из периметра длину стенки, например, 3 м. Получим результат: 15,1 – 3 = 12,1. В таком случае площадь составит 12,1 х 2,6 = 31,46 кв. м. Количество рулонов 31,46/4,13 = 8 штук.
- При выборе обоев длиной 15 м, количество полных полос из рулона будет 15/2,6 = 5, что составит площадь 0,53 х 5 = 2,65 кв. м. На нашу комнату понадобиться 15,1/2,65 = 6 рулонов.
В математике существует много способов расчета площадей фигур разной конфигурации. В наших рекомендациях указаны самые простые способы расчета площадей, как простых фигур (прямоугольника), так и более сложных (сегмента). Вооружитесь инструментом и терпением. У вас все получится.
Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
как посчитать, вычислить и узнать квадратуру пола. Как высчитать в квадратных метрах пол. Фото и видео
Содержание:
Невозможно проводить ремонт напольной поверхности, не зная точную площадь пола в частном домовладении или квартире. Дело в том, что сегодня стоимость строительных материалов достаточно высокая, и каждый владелец недвижимости старается максимально сэкономить на их покупке. Поэтому информация, как рассчитать площадь пола, не будет лишней для того, кто предпочитает делать ремонт собственноручно.
Зачем нужно знать площадь пола
Прежде чем приступить к работе, следует определиться с объемом мероприятий, запланировать затраты и рассчитать количество стройматериалов. Для этого нужны будут исходные данные. По этой причине важно знать, как посчитать площадь пола безошибочно. Особенно это касается неровных поверхностей и помещений, имеющих нестандартную планировку.
Встречаются и другие причины, когда имеется потребность точно определить размеры поверхности пола:
- проверка качества выполнения строительных работ;
- необходимость проведения перепланировки помещения.
В данной статье рассказывается, как посчитать площадь пола в квадратных метрах в комнатах, имеющих разную конфигурацию.
Определение площади прямоугольного помещения
До того, как высчитать площадь пола, следует запастись калькулятором и измерительной рулеткой. Чаще всего встречаются комнаты в форме прямоугольника. Для вычисления их площади пользуются формулой, известной всем со школы: S = a х b, где a и b – длина и ширина. Например, у помещения параметры 3 и 4 метра, тогда искомая величина составит 12 кв. м.
В том случае, когда в комнате имеется камин или встроенные предметы мебели, тогда нужно узнать их площадь и вычесть из общей площади. В случае проведения капитального ремонта пола, все лишнее в помещении придется демонтировать.
Расчет площади комнаты неправильной планировки
Намного труднее вычислить площадь комнаты, имеющей многоугольную форму. Часто в кирпичных домах в планировке присутствуют ниши, треугольные углубления и округлые элементы, как на фото.
В данном случае, прежде, как посчитать квадратуру пола, схему помещения надо разбить на отдельные зоны. Например, если комната имеет Г-образную планировку, ее следует поделить на 2 прямоугольника, после чего подсчитать площадь каждого из них и полученные результаты сложить.
Узнаём площадь треугольного помещения
Когда другая часть комнаты располагается не перпендикулярно относительно основной площади, это означает, что между двумя прямоугольниками присутствует еще и треугольник, имеющий прямой угол.
В данном случае площадь треугольника вычисляют по формуле: S = (a х b):2 и прибавляют к общему итогу. Например, а = 2, b = 3, тогда S = (2х3): 2 =3 м².
Можно иначе определить площадь:
- Прежде вычисляют квадрату прямоугольника.
- Определяют площадь скошенного треугольного угла.
- Из квадратуры прямоугольника вычитают площадь треугольника.
В том случае, когда треугольник не имеет прямого угла, тогда используют формулу Герона S = √p(p — a)(p — b)(p — c).
Например, стороны его равны 5, 6 и 7 метров, тогда вычисления производят следующим образом:
- Узнают полупериметр треугольника p = (5+6+7):2 = 9.
- В формулу Герона подставляют цифровые значения и получают результат: √(9 х(9-7) х(9-6)х(9-5) =14,7 м².
Квадратура помещений округлой формы
Нередко подобная форма присутствует у окон в домах старой постройки или на балконах, которые совмещены с комнатами. Сначала вычисляют 1/2 выступающей части окружности и добавляют к площади прямоугольника, применяя формулу S = πR²:2, в которой:
π = 3.14;
R² – радиус круга, возведенный в квадрат.
Например, в комнате имеется выступающий балкон полукруглой формы с радиусом 1,5 метра. Подставив данное число в формулу, получаем результат: S = 3,14х(1,5)²: 2 =3,5 м². Читайте также: «Как посчитать квадратные метры пола при разной форме комнат».
Как рассчитать площадь стен комнаты
Порядок вычисления площади стенок и пола отличается. Дело в том, что до того, как рассчитать квадратуру пола, следует узнать длину и ширину помещения, а для расчета стен потребуется измерить его высоту. Поэтому сначала узнают периметр комнаты и умножают на высоту потолков.
Например, параметры пола 3 и 4 метра, а высота помещения равна 3 метрам. В этом случае периметр стен будет равен (3 + 4) х2 = 14 м., а их площадь S = 14х3 = 42 м².
При этом не следует забывать про квадратуру проемов окон и дверей. Их площадь вычитают после завершения расчетов стен. Но с другой стороны их можно не принимать во внимание и тем самым обеспечить некоторый запас материалов.
Пропорции между площадью пола и окон
Согласно СНиП 31-01-2003 параметры окон и их количество должны зависеть от квадратуры пола. Так для жилых многоквартирных построек соотношение между площадями оконных проемов и напольной поверхности будет составлять, начиная от 1:5,5 до 1:8. Что касается верхних этажей, то там допускается минимальная пропорция 1:10.
Для частных домовладений эту норму регламентирует СНиП 31-02-2001. Согласно данной документации, на каждые 8 «квадратов» поверхности пола приходиться должно не менее одного «квадрата» источника естественного светового потока. На мансардных этажах эта пропорция не может быть менее 1:10.
Чтобы обеспечить качественное проведение ремонта нужно заранее выяснить, как вычислить площадь пола и другие необходимые размеры помещения. Подготовительный этап также предусматривает приобретение стройматериалов и тогда в процессе ремонта затраты будут сведены к минимуму, поскольку не получится больших остатков и стоимость доставки обойдется недорого.
Ручной способ вычислений как узнать площадь пола займет больше времени, чем при проведении расчетов на уже имеющемся строительном калькуляторе, но он позволяет узнать более точные результаты.
рассчитать с помощью онлайн калькулятора, найти, высчитать по формуле
Оглавление статьи:
Ремонт пола в квартире или доме требует точного расчета количества м2 в каждой комнате. В связи с тем, что на сегодняшний день строительные материалы – товар достаточно дорогой, каждый, кто затеял ремонт, пытается как можно больше сэкономить на материалах. Если вы не знаете, как правильно посчитать площадь неровного пола, который имеет нестандартные размеры – эта статья расскажет вам об этом.
Для чего могут пригодится расчеты?
Для чего нужно рассчитывать площадь пола:
- Чтобы купить необходимое количество материалов;
- Сэкономить на покупке напольного покрытия;
- Для того, чтобы определить количество жилой помощи в помещении;
- После строительства дома для определения соответствия с планом;
- При ремонте, для определения размеров будущей мебели и т. д;
Причин, по которым нужно вычислить площадь помещения – множество, решений же существует несколько.
Вычисление площади пола
Если комната стандартная (квадратная или прямоугольная), то вычислить площадь такого помещения сможет каждый. Для этого нужно узнать ширину и длину помещения, после чего просто перемножить эти показатели.
Таким образом, формула будет выглядеть так: S = a * b, где, а и b – длина и ширина помещения.
Если вы рассчитываете площадь помещения для потолка, то встроенные шкафы или камины никак не повлияют на замеры площади.
В случае, если вы собираетесь установить камин или же установить встроенный шкаф-купе, то площадь, которую он будет занимать, нужно обязательно вычислить исходя из предполагаемых размеров конструкции и общих размеров помещения.
Проводить точные замеры помещений, в которых имеется встроенная мебель, необходимо, если вы планируете укладывать напольное покрытие. В случае, если камин или комод занимает не много места, его площадью можно пренебречь, если много – конструкцию на время можно разобрать или высчитать сколько места она занимает.
Как высчитать площадь пола с неправильными размерами?
Если комната имеет нестандартные размеры – вычисление площади пола будет происходить немного дольше и сложнее. Существует множество причин, по которым комната может иметь нестандартные формы, например, ниша в спальне или встроенный шкаф. Стоит заметить, что способ найти площадь нестандартного пола все же можно. Для этого необходимо разбить помещение на небольшие геометрические фигуры, например, треугольники, квадраты, прямоугольники и т. д. Конечно, есть множество других способов, как рассчитать площадь пола, но с помощью такого способа – это сделать намного проще.
После того, как помещение будет разделено на геометрические фигуры, можно легко узнать их площадь, перемножив стороны одну на другую. После всех расчетов, площади фигур необходимо сложить, таким образом можно узнать точную площадь.
Среди прочих способов, как можно высчитать площадь пола, достаточно посмотреть жилую и общую площадь в домовой книге, если домовой книги нет – в плане застройщика.
Как вычислить площадь помещения, в котором есть скошенные углы?
Вычислить площадь помещения, в котором есть скошенный угол – достаточно просто, для этого нужно:
- Вычислить стороны треугольника;
- Рассчитать площадь по формуле S = (a*b)/2. В этом случае a и b – катеты треугольника.
Если треугольник не прямой, то рассчитать его площадь можно с помощью формулы Герона.
Формула Герона.Калькулятор расчета площади
Существует множество способов как найти площадь пола, одним из них является онлайн калькулятор, который позволит быстро и надежно рассчитать площадь любого помещения. От вас только требуется внести замеры в специальную таблицу.
Преимущества калькулятора расчета площади:
- Возможность высчитать площадь любой геометрической фигуры;
- Нет необходимости самостоятельно просчитывать;
- Скорость и точность расчетов.
Калькулятор расчета площади – это оптимальное решение вопроса, как быстро посчитать площадь пола комнаты.
Как посчитать необходимое количество плитки
Для того, чтобы узнать необходимое количество плитки, необходимой для укладки в той или иной комнате, необходимо узнать площадь помещения. Как быстро найти площадь пола любой комнаты – описано выше. После того, как площадь будет рассчитана, необходимо узнать площадь 1 плитки из выбранной коллекции. После этого нужно просчитать, сколько плиток необходимо для укладки её в комнате.
Пример:
- Площадь комнаты: 20 м2;
- Размеры плитки: 0,2 х 0,4 м;
- Площадь 1 плитки: 0,08 м2;
- Необходимое количество плиток: 250.
Таким способом можно узнать количество необходимой плитки. Таким же способом можно рассчитать необходимое количество паркетной доски или ламината. Стоит заметить, что в некоторых случаях количество необходимых материалов зависит от узора, который будет выполнен на напольной поверхности.
Советы
Для того, чтобы правильно рассчитать площадь пола – необходимо знать геометрические формулы или же уметь пользоваться онлайн калькулятором.
Данные по площади пола можно узнать из домовой книги. Комнаты, которые имеют сложную геометрическую форму проще всего рассчитывать с помощью деления их на небольшие геометрические объекты.
Узнать площадь полукруглой поверхности можно с помощью формулы: S = πR2/2 – радиус круга.
Для того, чтобы напольный материал не пришлось покупать еще – добавьте до необходимого количества 10%. Если вы правильно вычислите необходимое количество материалов – вы сможете качественно и надежно уложить любое напольное покрытие.
Как найти объем помещения. Как посчитать, посчитать количество места
Как посчитать, посчитать количество места.Оценка объема помещения часто требуется при производстве строительных и ремонтных работ. В большинстве случаев требуется указать количество материала, необходимое для проведения ремонта, а также для выбора эффективной системы отопления или кондиционирования. Количественные характеристики, описывающие пространство, обычно требуют несложных вычислений и измерений.
1. Самый простой случай — когда нужно определить объем правильной прямоугольной или квадратной формы комнаты. При использовании рулетки в метрах измеряют длину и ширину стен, а также высоту помещения. Самый удобный способ проводить замеры на полу, вдоль плинтусов. Умножьте полученную длину на ширину, высоту и получите желаемую сумму.
2. Если комната неправильной или сложной формы, задача несколько сложнее.Разделите площадь пола на несколько простых фигур (прямоугольники, квадраты, полукруги и т. Д.) И вычислите площадь каждой из них, произведя предварительное измерение. Сложите полученные значения, суммируя площадь. Умножьте сумму высоты помещения. Измерения следует проводить в одних и тех же единицах измерения, например, в метрах.
3. При проведении строительных работ определение объема всей конструкции определяется стандартами. Так называемый строительный объем наземной части здания с мансардой можно рассчитать, умножив площадь горизонтального сечения с внешней стороны на уровень нижнего этажа.Измерьте общую высоту здания от уровня готового пола до верхней части утеплителя мансардного этажа. Умножьте оба значения.
4. При наличии разных площадей общей площади в здании определить, сложить количество всех частей. Так же определяется объем, если помещения имеют разную форму и дизайн.
5. Отдельно рассчитать объем веранд, эркеров, тамбур и других конструкций вспомогательных элементов (кроме внутреннего и наружного балконов).Включите эту информацию в общий объем всех помещений здания. Таким образом, вы легко сможете найти количество любого помещения или здания, расчеты достаточно просты, постарайтесь и будьте внимательны.
формула объема помещения
формула ПРИМЕР Формула расчета объема помещения Калькулятор площади стены или полаВставьте размеры помещения и получите результат.
Калькулятор объема
Ниже приводится список калькуляторов объема для нескольких распространенных форм.Заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор объема куба
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.
Калькулятор объема конической ствола
Калькулятор объема эллипсоида
Калькулятор объема квадратной пирамиды
Калькулятор объема трубки
Калькулятор площади сопутствующих поверхностей | Калькулятор площади
Объем — это количественная оценка трехмерного пространства, которое занимает вещество.Единицей измерения объема в системе СИ является кубический метр, или м 3 . Обычно объем контейнера — это его вместимость и количество жидкости, которое он может вместить, а не количество места, которое фактически вытесняет контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере составляет радиус r .Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема шара приведено ниже:
EX: Клэр хочет заполнить идеально сферический воздушный шар с радиусом 0.15 футов с уксусом для борьбы с ее заклятым врагом Хильдой на воздушных шарах в предстоящие выходные. Необходимый объем уксуса можно рассчитать, используя приведенное ниже уравнение:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован так же, как круг, набором отрезков прямых, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или другое основание).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полукруглых линий, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:
, где r — радиус, а h — высота конуса
EX: Би полна решимости выйти из магазина мороженого, не зря потратив свои с трудом заработанные 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что на 15% предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15% больше, чем у сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью следующего уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйм 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет <15%, и решает купить сахарный рожок.Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое из контейнеров в ее рожок.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых пересекаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб является частным случаем многих классификаций геометрических фигур, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:
объем = 3
где a — длина ребра куба
EX: Боб, который родился в Вайоминге (и никогда не покидал штат), недавно посетил свою исконную родину, Небраску. Пораженный великолепием Небраски и окружающей средой, непохожей на какие-либо другие, с которыми он когда-либо сталкивался, Боб знал, что он должен привезти с собой домой часть Небраски. У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от данной прямой оси.Однако в обычном использовании «цилиндр» относится к правильному круговому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником рециркуляции, он извлек три цилиндрических бочки с незаконной свалки и очистил бочки от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который каждая может вместить, используя следующее уравнение:
объем = π × 3 2 × 4 = 113.097 футов 3
Он успешно строит замок из песка в своем доме и в качестве дополнительного бонуса экономит электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.
Прямоугольный резервуар
Прямоугольный резервуар — это обобщенная форма куба, стороны которого могут иметь различную длину. Он ограничен шестью гранями, три из которых пересекаются в его вершинах, и все они перпендикулярны своим соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к торту.Она планирует отправиться в поход по тропе Калалау на Кауаи, и, хотя она в очень хорошей форме, Дарби беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может уместить в свою упаковку, рассчитан ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула — это трехмерная геометрическая форма, состоящая из цилиндра и двух полусферических концов, где полусфера — это полусфера.Отсюда следует, что объем капсулы можно рассчитать, объединив уравнения объема для сферы и правого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + ч) |
, где r — радиус, а h — высота цилиндрической части
EX: Имея капсулу радиусом 1,5 фута и высотой 3 фута, определите объем растопленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет похоронить для будущих поколений на пути к самопознанию. Гималаи:
объем = π × 1.5 2 × 3 + 4/3 × π × 1,5 3 = 35,343 фута 3
Сферический колпачок
Сферический колпачок — это часть сферы, отделенная от остальной сферы плоскостью. Если плоскость проходит через центр сферы, сферический колпачок называется полусферой. Существуют и другие различия, включая сферический сегмент, где сфера сегментирована двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферической крышки выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, указанной в калькуляторе:
Для двух значений предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Для r и R : h = R ± √R 2 — r 2
где r, — радиус основания, R — радиус сферы, а h — высота сферической крышки.
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, решает саботировать мяч для гольфа Джеймса.Он отрезает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса и ему нужно рассчитать объем материала, необходимый для замены сферической крышки и перекоса веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К несчастью для Джека, за день до игры Джеймс получил новую партию мячей, и все усилия Джека были напрасны.
Коническая Frustum
Усеченный конус — это часть твердого тела, которая остается при разрезании конуса двумя параллельными плоскостями. Этот калькулятор рассчитывает объем специально для правильного кругового конуса. Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:
| объем = | πh (r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
EX: Би успешно приобрела мороженое в сахарном рожке и только что съела его таким образом, чтобы мороженое оставалось упакованным внутри рожка, а поверхность мороженого была ровной и параллельной плоскости отверстия рожка.Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть дна рожка, которая идеально параллельна ранее единственному отверстию. Теперь у Би есть усеченная пирамида правой конической формы, из которой вытекает мороженое, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченной кости 4 дюйма с радиусом 1,5 дюйма и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 в 3
Эллипсоид
Эллипсоид является трехмерным аналогом эллипса и представляет собой поверхность, которую можно описать как деформацию сферы посредством масштабирования элементов направления. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки прямых, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:
, где a , b и c — длины осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и позволяет ему есть столько мяса, сколько он может уместить в булочке в форме эллипса. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может уместить в своем сэндвиче. Учитывая, что его булочка имеет длину оси 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат рассчитывает объем мяса, который он может уместить в каждой полой булочке, следующим образом:
объем = 4/3 × π × 1.5 × 2 × 5 = 62,832 дюйма 3
Квадратная пирамида
Пирамида в геометрии — это трехмерное твердое тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это форма на плоскости, ограниченная конечным числом отрезков прямых линий. Существует много возможных многоугольных оснований пирамиды, но квадратная пирамида — это пирамида, в которой основание представляет собой квадрат. Еще одно отличие пирамид заключается в расположении вершины. У правых пирамид есть вершина, которая находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды может быть записан как:
Объем обобщенной пирамиды:
, где b — площадь основания, а h — высота
Объем квадратной пирамиды:
, где a — длина края основания
EX: Ван очарован Древним Египтом и особенно любит все, что связано с пирамидами.Будучи старшим из своих братьев и сестер Ту, Дерево и Форе, он может легко загонять и развертывать их по своему желанию. Воспользовавшись этим, Ван решает воссоздать древнеегипетские времена, а его братья и сестры выступают в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать, используя уравнение для квадрата. пирамида:
объем = 1/3 × 5 2 × 12 = 100 футов 3
Трубчатая пирамида
Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газа.Для вычисления объема трубы используется та же формула, что и для цилиндра (объем = pr 2 h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего. С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
, где d 1 — внешний диаметр, d 2 — внутренний диаметр, а l — длина трубки
EX: Beulah посвящен охране окружающей среды.Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу через ручей. Ему нужен более легкий доступ к своему дому, и он просит Беулу построить ему дорогу, следя за тем, чтобы ручей мог течь свободно, чтобы не мешать его любимому месту рыбалки. Она решает, что надоедливые бобровые дамбы будут хорошей отправной точкой для прокладки трубы через ручей. Объем запатентованного бетона с низкой ударопрочностью, необходимый для строительства трубы с внешним диаметром 3 фута и внутренним диаметром 2.5 футов и длина 10 футов можно рассчитать следующим образом:
| объем = π × | × l0 = 21,6 футов 3 |
Единицы измерения общего объема
| Единица | кубических метров | миллилитров |
| миллилитров (кубических сантиметров) | 0,000001 | 1 |
| кубических дюймов | 0,00001639 | 16,39 |
| пинт | 0.000473 | 473 |
| кварта | 0,000946 | 946 |
| литр | 0,001 | 1,000 |
| галлон | 0,003785 | 3,785 |
| 0,03 | 39||
| кубический ярд | 0,764555 | 764,555 |
| кубический метр | 1 | 1,000,000 |
| кубический километр | 1,000,000,000 | 10 15 |
Расчетный объем | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, т.е.е. насколько вы могли бы поместиться в предмет, если бы, например, вы залили его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.
В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.
Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько у вас есть места для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.
Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда говорят о пропускной способности плотины или течении реки.
Примечание к агрегатам
Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.
Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе. Кубические единицы включают см 3 , м 3 и кубические футы.
ВНИМАНИЕ!
Объем также можно выразить как вместимость по жидкости.
Метрическая система
В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см 3 .1 литр = 1000 мл = 1000 см 3 .
Британская / английская система
В британской / английской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше придерживаться жидких или твердых единиц объема.
Подробнее см. На нашей странице Системы измерения
Основные формулы для расчета объема
Объем прямоугольных тел
В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
То, как вы относитесь к различным размерам, не меняет расчет: например, вы можете использовать «глубину» вместо «высоты». Важно то, что все три измерения умножаются. Вы можете умножать в любом порядке, поскольку это не изменит ответ (подробнее см. Нашу страницу о умножении ).
Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3
Объем призм и цилиндров
Эта базовая формула может быть расширена для охвата цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.
Таким образом, основная формула для определения объема призм и цилиндров:
Площадь формы торца × высота / глубина призмы / цилиндра.
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для вычисления объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем — это только часть общей суммы, которая была бы, если бы они продолжались. в той же форме насквозь.
Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.
Таким образом, формула:
Площадь основания или торца × высота конуса / пирамиды × 1 / 3
Вернитесь на нашу страницу Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:Площадь внутри круга = πr2 (где π (пи) приблизительно равно 3.14 и r — радиус окружности).
В этом примере площадь основания (круга) = πr 2 = 3,14 × 5 × 5 = 78,5 см 2 .
78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3
Объем сферы
Как и в случае с кругом, вам нужно π (пи) для вычисления объема сферы.
Формула: 4/3 × π × радиус 3 .
Вам может быть интересно, как определить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть способ попроще.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности рассчитывается как 2 x π x радиус.
Чтобы вычислить радиус из окружности, вы:
Разделите окружность на (2 x π) .
Рабочие примеры: Расчет объема
Пример 1
Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.
Сначала определите площадь одного из круглых концов цилиндра.
Площадь круга равна πr 2 (π × радиус × радиус). π (пи) приблизительно равно 3,14.
Таким образом, площадь конца равна:
3.14 x 2,5 x 2,5 = 19,63 см 2
Объем — это площадь конца, умноженная на длину, и, следовательно, составляет:
19,63 см 2 x 20 см = 392,70 см 3
Пример 2
Что больше по объему: сфера радиусом 2 см или пирамида с основанием в квадрате 2,5 см и высотой 10 см?
Сначала определим объем сферы .
Объем сферы составляет 4/3 × π × радиус 3 .
Таким образом, объем сферы равен:
.4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3
Затем определите объем пирамиды .
Объем пирамиды 1/3 × площадь основания × высота.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2
Объем, следовательно, равен 1/3 x 6,25 × 10 = 20.83 см 3
Таким образом, сфера больше по объему, чем пирамида.
Расчет объема твердых тел неправильной формы
Точно так же, как вы можете вычислить площадь неправильных двумерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.
Рабочий пример
Рассчитайте объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью.
Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).
Объем сферы составляет 4/3 × π × радиус 3 . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть является полусферической, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:
.0,5 × 4/3 × π × 203 = 16,755,16 см 3
Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь цоколя πr 2 .
Таким образом, объем цилиндрического сечения данной формы равен:
80 × π × 20 × 20 = 100 530,96 см 3
Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см 3 ). Однако вполне правильно выразить его как cm 3 , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.
Дополнительная литература по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Если вы хотите освежить в памяти основы или помочь своим детям в обучении, эта книга для вас.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.
Калькулятор объема.Определение | Формулы
Калькулятор объема рассчитает объем некоторых из наиболее распространенных трехмерных твердых тел. Прежде чем мы перейдем к тому, как рассчитать объем, вы должны знать определение объема. Объем отличается от площади, которая представляет собой объем пространства, занимаемого двухмерной фигурой. Поэтому вы можете быть сбиты с толку относительно того, как найти объем прямоугольника по сравнению с тем, как найти объем коробки. Калькулятор поможет вычислить объем сферы, цилиндра, куба, конуса и прямоугольных тел.
Что такое объем? Определение объема
Объем — это объем пространства, занимаемого объектом или веществом. Обычно под объемом контейнера понимается его вместимость, а не пространство, которое сам контейнер перемещает. Кубический метр (м 3 ) — это единица измерения объема в системе СИ.
Однако термин том может также относиться ко многим другим вещам, например,
- степень громкости или интенсивность звука (вы можете проверить наш калькулятор шумового загрязнения или калькулятор дБ)
- количество или количество чего-либо (обычно большого количества)
- формальное слово для книги или одной из набора связанных книг.
Единицы измерения объема, таблица пересчета
Популярные единицы объема:
- Метрические единицы объема
- кубических сантиметров (см³)
- кубических метров (м³)
- литров (л, л)
- миллилитров (мл, мл)
- Стандарт США, Великобритания
- жидкая унция (жидкая унция)
- кубических дюймов (у.е.)
- кубических футов
- стаканов
- пинт (pt)
- кварты (кварты)
- галлонов (гал.)
Если вам нужно преобразовать единицы объема, вы можете использовать наш конвертер больших объемов.Еще один полезный инструмент — наш калькулятор граммов в чашки, который может помочь, если вы хотите использовать рецепт еды из другой страны. Обратите внимание, что это не простое преобразование, а переход от веса (граммы) к единице объема (чашки) — поэтому вам нужно знать тип ингредиента (или, точнее, его плотность).
Кроме того, вы можете взглянуть на эту аккуратную таблицу преобразования единиц объема, чтобы узнать коэффициент преобразования в мгновение ока:
| кубических дюймов | кубических футов | кубических ярдов | галлонов жидкости сша | галлонов сша | imp жидких галлонов | баррелей (нефть) | чашек | жидких унций (Великобритания) | жидких унций (США) | пинт (Великобритания) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| куб.м | 6.1 10 4 | 35,3 | 1,30 8 | 264,2 | 227 | 220 | 6,29 | 4227 | 3,52 10 4 | 3,38 10 4 | 1760 |
| кубический дециметр | 61.02 | 0,035 | 1,3 10 -3 | 0,264 | 0,227 | 0,22 | 0,006 | 4,23 | 35,2 | 33,8 | 1,76 |
| кубический сантиметр | 0.061 | 3,5 10 -5 | 1,3 10 -6 | 2,64 10 -4 | 2,27 10 -4 | 2,2 10 -4 | 6,29 10 -6 | 4,2 10 -3 | 3,5 10 -2 | 3.34 10 -2 | 1,76 10 3 |
| кубический миллиметр | 6,1 10 -5 | 3,5 10 -8 | 1,31 10 -9 | 2,64 10 -7 | 2,27 10 -7 | 2,2 10 -7 | 6.3 10 -9 | 4,2 10 -6 | 3,5 10 -5 | 3,4 10 -5 | 1,76 10 -6 |
| гектолитров | 6,1 10 3 | 3,53 | 0,13 | 26.4 | 22,7 | 22 | 0,63 | 423 | 3,5 10 3 | 3381 | 176 |
| литров | 61 | 3,5 10 -2 | 1.3 10 -3 | 0,26 | 0,23 | 0,22 | 6,3 10 -3 | 4,2 | 35,2 | 33,8 | 1,76 |
| сантилитров | 0,61 | 3.5 10 -4 | 1,3 10 -5 | 2,6 10 -3 | 2,3 10 -3 | 2,2 10 -3 | 6,3 10 -5 | 4,2 10 -2 | 0,35 | 0,338 | 1.76 10 -2 |
| миллилитры | 6,1 10 -2 | 3,5 10 -5 | 1,3 10 -6 | 2,6 10 -4 | 2,3 10 -4 | 2,2 10 -4 | 6,3 10 -6 | 4.2 10 -3 | 3,5 10 -2 | 3,4 10 -2 | 1,76 10 -3 |
| куб. Дюймов | 1 | 5,79 10 -4 | 2,1 10 -5 | 4,3 10 -3 | 3.7 10 -3 | 3,6 10 -3 | 10 -4 | 6,9 10 -2 | 0,58 | 0,55 | 2,9 10 -2 |
| кубических футов | 1728 | 1 | 0.037 | 7,48 | 6,43 | 6,23 | 0,18 | 119,7 | 997 | 958 | 49,8 |
| кубических ярдов | 4,7 10 4 | 27 | 1 | 202 | 173.6 | 168,2 | 4,8 | 3232 | 2,69 10 4 | 2,59 10 4 | 1345 |
| сша жидких галлонов | 231 | 0,134 | 4,95 10 -3 | 1 | 0.86 | 0,83 | 0,024 | 16 | 133,2 | 128 | 6,7 |
| сша галлонов сухой | 268,8 | 0,156 | 5,76 10 -3 | 1.16 | 1 | 0,97 | 0,028 | 18,62 | 155 | 148,9 | 7,75 |
| imp жидкие галлоны | 277,4 | 0,16 | 5,9 10 -3 | 1.2 | 1.03 | 1 | 0,029 | 19,2 | 160 | 153,7 | 8 |
| баррелей (нефть) | 9702 | 5,61 | 0,21 | 42 | 36.1 | 35 | 1 | 672 | 5596 | 5376 | 279,8 |
| стаканов | 14,4 | 8,4 10 -3 | 3,1 10 -4 | 6.2 10 -2 | 5,4 10 -2 | 5,2 10 -2 | 1,5 10 -3 | 1 | 8,3 | 8 | 0,4 |
| жидких унций (Великобритания) | 1,73 | 10-3 | 3.7 10 -5 | 7,5 10 -3 | 6,45 10 -3 | 6,25 10 -3 | 1,79 10 -4 | 0,12 | 1 | 0,96 | 5 10 -2 |
| жидких унций (США) | 1.8 | 10 -3 | 3,87 10 -5 | 7,8 10 -3 | 6,7 10 -3 | 6,5 10 -3 | 1,89 10 -4 | 0,13 | 1,04 | 1 | 0.052 |
| пинт (Великобритания) | 34,7 | 0,02 | 7,4 10 -4 | 0,15 | 0,129 | 0,125 | 3,57 10 3 | 2,4 | 20 | 19.2 | 1 |
Как рассчитать объем? Формулы объема
На этот вопрос нет простого ответа, так как он зависит от формы рассматриваемого объекта. Вот формулы для некоторых наиболее распространенных форм:
Куб =
с³, где с — длина стороны.Сфера =
(4/3) πr³, где r — радиус.Цилиндр =
πr²h, где r — радиус, а h — высота.Конус =
(1/3) πr²h, где r — радиус, а h — высота.Прямоугольное тело (объем ящика) =
lwh, где l — длина, w — ширина и h — высота (примером такой формы может служить простой бассейн).Пирамида =
(1/3) Ah, где A — площадь основания, а h — высота. Для пирамиды с правильным основанием также можно использовать другое уравнение: Пирамида =(n / 12) * h * длина_сокры ² * кроватка (π / n), где n — количество сторон основания для правильный многоугольник.Призма =
πAh, где A — площадь основания, а h — высота. Для прямоугольной призмы уравнение можно легко вывести, как и для правой прямоугольной призмы, которая, по-видимому, имеет ту же форму, что и прямоугольник.
| Форма | Имя | Формула |
|---|---|---|
| Куб | В = с³ | |
| Прямоугольная призма правая (прямоугольная, прямоугольная) | В = л / ч | |
| Призма или цилиндр | В = Ач | |
| Пирамида или конус | В = Ач / 3 | |
| Сфера | В = 4πr³ / 3 |
Калькулятор объема и инструменты, предназначенные для определенных форм
Мы решили сделать из этого калькулятора объема простой инструмент, охватывающий пять самых популярных трехмерных фигур.Однако не все уравнения объема и формы могут быть реализованы здесь, так как это сделает калькулятор перегруженным и не интуитивно понятным. Так что, если вы ищете конкретную форму, ознакомьтесь с калькуляторами, посвященными объемам выбранных форм:
Калькулятор объема — как использовать
Давайте посмотрим на примере использования этого калькулятора объема:
Выберите тип 3D-формы . Если вы не можете найти форму, объем которой хотите рассчитать, выберите другие специальные специальные калькуляторы (ссылки вы найдете выше).В этом примере предположим, что вы хотите рассчитать объем цилиндра.
Выберите правый раздел калькулятора объема . В нашем случае это деталь с названием Объем цилиндра .
Введите данные в соответствующие поля . Наш цилиндр имеет радиус 1 фут и высоту 3 фута. Вы можете изменить единицы измерения простым щелчком по названию единицы.
Поехали! Объем выбранной формы отображается .В нашем случае это 9,42478 куб. Футов
Если вы хотите проверить, сколько это в баррелях США, просто нажмите на название единицы и выберите бочки из раскрывающегося списка. Наш цилиндр имеет емкость ~ 2,24 баррелей масла.
Измерение объема твердых тел, жидкостей и газов
Как найти объем объектов с разным состоянием материи?
- Цельный
Итак, если вы хотите измерить объем необычного объекта, просто следуйте по стопам Архимеда (хотя вы можете опустить часть «голая гонка»):
Возьмите емкость больше, чем объект, объем которого вы хотите измерить, .Это может быть ведро, мерный стаканчик, стакан или мерный цилиндр. На нем должна быть шкала.
Налейте воду в емкость и снимите показания объема.
Поместите объект внутрь . Он должен быть полностью погружен для измерения всего объема объекта. Прочтите том. Этот метод не сработает, если ваш объект растворяется в воде.
Разница между измерениями — это объем нашего объекта.
Эти измерения необходимы для расчета выталкивающей силы, основанной на принципе Архимеда.
- Жидкость
Обычно измерить объем жидкости довольно просто — все, что вам нужно, — это какой-нибудь мерный сосуд с градуировкой. Выберите тот, который соответствует вашим потребностям: необходимо учитывать количество жидкости и степень точности. Емкости, используемые для выпечки торта (посмотрите отличный калькулятор для рецепта блинов), будут отличаться от тех, что используются в химии (например.г. в расчетах молярной концентрации) будет отличаться от тех, которые используются в медицинских целях (например, доза лекарства).
- Газ
Мы должны использовать более сложные методы для измерения объема газа. Вы должны помнить, что на объем газа влияют температура и давление, и что газы расширяются, чтобы заполнить любой контейнер, в который они помещены. Вы можете попробовать измерить это:
Надуйте баллон газом, который вы хотите измерить (например,г., с гелием, чтобы поднять вас в воздух). Затем можно воспользоваться методом Архимеда — опустить баллон в ведро с водой и проверить разницу объемов. Вы найдете подробные инструкции на странице wikihow.
Проверьте показатели, связанные с объемом легких, с помощью прибора под названием спирометр .
В химии, газовый шприц используется для ввода или отбора объема газа из закрытой системы . Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции.
Или рассчитать :
Найдите объем газа, , учитывая его плотность и массу . Используйте простое уравнение объема
V = m / d.Рассчитайте объем сжатого газа в баллоне, используя уравнение идеального газа.
Как найти объем * прямоугольника * по сравнению с объемом * коробки *
Вы не можете рассчитать объем прямоугольника , объем круга или объем квадрата, потому что это двухмерные геометрические фигуры.Таким образом, прямоугольник не имеет объема (но имеет площадь). Вероятно, вы ищете объем прямоугольного кубоида (или, говоря более общим языком, вы хотите найти объем коробки), который представляет собой трехмерный объект.
Чтобы найти объем коробки, просто умножьте длину, ширину и высоту — и готово! Например, если размер коробки 5х7х2 см, то объем коробки составляет 70 кубических сантиметров. Для размеров, которые представляют собой относительно небольшие целые числа, легко вычислить объем вручную.Для больших или десятичных чисел использование калькулятора объема очень эффективно.
В реальной жизни есть много приложений, в которых можно использовать калькулятор объема. Один из таких примеров — строительство дорог или тротуаров, где должны быть построены бетонные плиты. Как правило, бетонные плиты представляют собой твердые тела прямоугольной формы, поэтому можно использовать калькулятор бетона, который является приложением калькулятора объема.
Также формулы объема могут быть полезны, если вы увлеченный садовник или просто счастливый обладатель дома с двором.Ознакомьтесь с нашими замечательными инструментами, такими как:
Более того, вы можете встретить том на своей кухне или в ванной: для любой жидкости, которую мы пьем (например, воды в бутылках), а также косметических товаров или зубной пасты, на упаковке продукта указан объем (в миллилитрах / литрах или жидких унциях). / галлоны).
Еще одно родственное приложение, хотя и немного другое, — это концепция площади поверхности. Предположим, что весь фасад здания должен быть окрашен. Чтобы знать, сколько нужно приобрести краски, необходимо рассчитать площадь здания.Удобный в использовании калькулятор площади рассчитает это за вас.
FAQ
Как найти объем?
Формула объема зависит от формы объекта . Одной из самых популярных форм является прямоугольная призма, также известная как коробка, где вы можете просто умножить длину на ширину на высоту , чтобы найти ее объем. Другой распространенной формой является цилиндр — чтобы найти его объем, умножьте высоту цилиндра на площадь его основания (π ⨉ r 2 ).Для других трехмерных фигур проверьте Калькулятор объема Omni.
Как измерить объем?
Измерение объема зависит от состояния вещества вашего объекта. Для жидкостей вы можете использовать мерный цилиндр или бюретку для измерений в химической лаборатории или мерный стакан и ложку для повседневных целей. Что касается газов, чтобы приблизительно измерить объем, вы можете надуть баллон и использовать его для вытеснения воды в мерном цилиндре. Аналогичный метод работает для твердых тел — поместите объект в градуированный контейнер и измерьте изменение показаний.
Объем — квадрат или куб?
Объем кубический, так как это трехмерная мера. Площадь — это «квадратное» значение, поскольку площадь фигуры охватывает два измерения. Вы можете вспомнить, что объем представляет собой кубическое значение, вспомнив несколько названий единиц объема, например, кубических метра , кубических футов или кубических ярдов .
Как рассчитать объем?
В зависимости от формы объекта вы можете использовать разные формулы для расчета объема:
- Объем куба = сторона 3 .
- Кубоид (прямоугольная коробка) объем = длина ⨉ ширина ⨉ высота
- Объем сферы = (4/3) ⨉ π ⨉ радиус 3
- Объем цилиндра = π ⨉ радиус 2 ⨉ высота
- Объем конуса = (1/3) ⨉ π ⨉ радиус 2 ⨉ высота
- Объем пирамиды = (1/3) площадь основания ⨉ высота
В чем измеряется объем?
Кубический метр — единица объема в системе СИ.Однако, поскольку это непрактично, чаще всего вы можете встретить объем, выраженный в:
.- Кубические сантиметры
- Кубические дюймы
- Миллилитры
- литров
- галлонов
Как найти объем жидкости?
Градуированные цилиндры и Колбы Эрленмейера подойдут, если вам нужно приблизительно измерить объем жидкости. Для более точных измерений нужно использовать мерную пипетку и бюретку.Однако, если вы печете торт или готовите вкусное блюдо и в рецепте используются единицы объема, вы можете просто использовать мерный стакан, стакан или ложку.
Какая единица измерения объема в системе СИ?
Кубический метр (м 3 ) — это единица измерения объема в системе СИ. Он образован от основной единицы измерения длины в системе СИ — метра. Хотя кубический метр является базовой единицей СИ, чаще используются другие единицы: для метрической системы популярны миллилитры, литры или кубические сантиметры, а для имперской системы вы можете найти объем, выраженный в пинтах, галлонах, кубических дюймах и т. Д. кубические футы или кубические ярды.
Объем интенсивный или экстенсивный?
Объем — это обширное свойство , такое же, как количество вещества, массы, энергии или энтропии. Обширное свойство — это мера, в которой зависит от количества вещества . Посмотрите на этот пример: стакан, бочка и бассейн, полный воды, имеют разные объемы и массы ( обширных свойства ), но вода в этих трех контейнерах будет иметь одинаковую плотность, показатель преломления и вязкость ( интенсивных свойств ). ).
В чем разница между площадью поверхности и объемом?
Объем — это трехмерная мера , а площадь поверхности — двумерная . Объем сообщает нам о кубическом пространстве, которое занимает объект, а площадь поверхности — это сумма всех областей, образующих трехмерную форму. Возьмем, например, картонную коробку 📦:
- Объем — это объем места, занимаемого коробкой, просто это места, доступное внутри коробки
- Площадь поверхности — это пространство , занимаемое сторонами коробки , вычисленное при покраске сторон или упаковке коробки в бумагу.
Как найти объем объекта неправильной формы?
Вы можете использовать метод вытеснения жидкости для твердых объектов неправильной формы:
- Наполните емкость водой и отметьте уровень воды.
- Бросьте ваш объект внутрь и снова отметьте уровень. Убедитесь, что ваш предмет не растворяется в воде.
- Для масштабированных контейнеров вы можете всего вычесть исходного объема из нового объема. И все, поздравляю!
Но если на вашем оригинальном контейнере нет весов:
- Вынести предмет.
- Наполните вашу емкость водой до второй отметки, залейте этой воды в мерный цилиндр / другую мерную емкость.
- Повторите шаг 6 для другого отмеченного уровня и вычтите объемы.
- Пэт себе на спину — вы нашли объем объекта неправильной формы!
Что измеряет объем?
Объем измеряет пространства, занимаемого объектом в трех измерениях .Еще один близкий термин — вместимость, то есть объем внутреннего пространства объекта. Другими словами, вместимость описывает, сколько контейнер может вместить (воды, газа и т. Д.).
Каков объем Земли?
Объем Земли примерно равен 1,08321 × 10 12 км 3 ( 1,08 квадриллион кубических километров ), или 2,59876 × 10 11 кубических миль ( 259 триллионов кубических миль ). Вы можете получить этот результат, используя формулу объема сферы (4/3) ⨉ π ⨉ radius 3 и предполагая, что средний радиус Земли составляет 6371 километр (3958.76 миль).
Как рассчитать отношение площади поверхности к объему?
Чтобы вычислить отношение площади поверхности к объему SA: V, вы просто разделите площадь поверхности на объема. Для некоторых выбранных форм:
- Соотношение SA: V для куба = (сторона 6 ⨉ 2 ) / (сторона 3 ) = 6 / сторона
- Отношение SA: V для сферы = (4 ⨉ π ⨉ радиус 2 ) / ((4/3) ⨉ π ⨉ радиус 3 ) = 3 / радиус
- Соотношение SA: V для цилиндра = (2 ⨉ π ⨉ радиус 2 + 2 ⨉ π ⨉ радиус ⨉ высота) / (π ⨉ радиус 2 ⨉ высота) = 2 ⨉ (радиус + высота) / ( радиус ⨉ высота)
Используйте расчет изменений воздуха для определения помещения CFM
Инженерный воздушный поток в помещении может представлять реальную проблему при балансировке системы отопления, вентиляции и кондиционирования воздуха.В большинстве расчетов для определения необходимого расхода воздуха используются только теплопотери или прирост в помещении, и часто не принимаются во внимание потребности в вентиляции помещения. Давайте посмотрим, как расчет воздухообмена может упростить этот этап балансировки воздуха.
Что такое воздухообмен?
Воздухообмен — это количество раз, когда воздух входит и выходит из комнаты из системы HVAC за один час. Или сколько раз комната заполнялась воздухом из регистров приточного воздуха за шестьдесят минут.
Затем вы можете сравнить количество изменений воздуха в помещении с приведенной ниже таблицей требуемых изменений воздуха. Если он находится в допустимом диапазоне, вы можете приступить к проектированию или уравновешиванию воздушного потока и получить дополнительную уверенность в том, что вы все делаете правильно. Если это выходит за пределы досягаемости, вам лучше еще раз взглянуть.
Формула изменения воздуха
Чтобы рассчитать воздухообмен в помещении, измерьте приток воздуха в комнату, умножьте CFM на 60 минут в час. Затем разделите на объем комнаты в кубических футах:
Говоря простым языком, мы заменяем CFM на кубические футы в час (CFH).Затем мы вычисляем объем комнаты, умножая высоту комнаты на ширину и длину. Затем просто делим CFH на объем помещения.
Вот пример того, как работает полная формула:
Теперь сравните 7,5 воздухообменов в час с необходимыми воздухообменами для этого типа помещения в таблице воздухообменов в час ниже . Если это комната для обеда или отдыха, где требуется 7-8 воздухообменов в час, вы точно попали в цель. Если это бар, который требует 15-20 воздухообменов в час, пора подумать.
Комнатная формула CFM
Давайте посмотрим на эту инженерную формулу по-другому. Например, что, если воздушный поток неизвестен, и вам нужно рассчитать необходимый CFM для комнаты? Вот четырехэтапный процесс расчета CFM помещения:
Шаг первый — Используйте приведенную выше таблицу изменения воздуха в час , чтобы определить требуемые изменения воздуха, необходимые для использования помещения. Допустим, это конференц-зал, требующий 10 воздухообменов в час.
Шаг второй — Рассчитайте объем комнаты (ДхШхВ).
Шаг третий — Умножьте объем помещения на требуемый объем воздухообмена.
Шаг четвертый. Разделите ответ на 60 минут в час, чтобы найти нужную комнату. CFM:
Вот пример того, как работать по формуле:
При проектировании или балансировке системы, требующей дополнительного воздушного потока для вентиляции, помните, что в этой комнате обычно требуется постоянная работа вентилятора, когда она занята.Это может представлять проблему для других комнат в той же зоне, поэтому примите это во внимание.
Для многих из этих помещений может потребоваться значительное количество наружного воздуха. Содержание БТЕ в этом воздухе должно быть включено в приток тепла или теплопотери здания при определении размера оборудования для обогрева и охлаждения.
Попрактикуйтесь в этих расчетах несколько раз в магазине или офисе. Затем выполните расчеты в полевых условиях несколько раз в течение следующей недели, чтобы проверить воздушный поток в помещениях с необычными требованиями к вентиляции. Изучите изменения воздуха в час в таблице , чтобы ознакомиться с помещениями, в которых требуется больше вентиляции, чем требуется для обогрева или охлаждения.
R ob «Doc» Falke обслуживает промышленность в качестве президента National Comfort Institute, обучающей компании и членской организации, работающей в сфере отопления, вентиляции и кондиционирования воздуха. Если вы подрядчик или технический специалист по ОВКВ, заинтересованный в бесплатной процедуре расчета замены воздуха, свяжитесь с Доком по телефону robf @ ncihvac.com или позвоните ему по телефону 800-633-7058. Посетите веб-сайт NCI по адресу nationalcomfortinstitute.com для получения бесплатной информации, статей и загрузок.
Калькулятор воздухообмена в час (формула на основе CFM)
ACH или A ir C hanges P er H наш — это показатель, который показывает нам, сколько раз устройство HVAC может заполнить воздухом весь объем помещения. Это особенно полезно при сравнении различных очистителей воздуха или кондиционеров.
Пример: Давайте возьмем очиститель воздуха с расходом воздуха 250 куб. Футов в минуту. Мы поместили его в комнату площадью 200 кв. Футов с потолком стандартной высоты (8 футов). Сколько воздухообменов в час производит установка?
Расчет: 250 кубических футов в минуту — 250 кубических футов в минуту. За один час (60 минут) мы получаем 60 * 250 = 15 000 кубических футов в час. Общий объем комнаты составляет 200 квадратных футов * 8 футов = 1600 кубических футов. Такой очиститель воздуха способен полностью изменить объемный воздух в помещении 15.000 / 1,600 = 9,375 раз.
Ответ: ACH = 9,375
Вот удобный калькулятор воздухообмена в час, которым вы можете свободно пользоваться. Просто укажите площадь, высоту потолка и CFM рассматриваемого устройства HVAC, и вы сможете рассчитать ACH:
.Калькулятор ACH
Формула (рассчитать ACH самостоятельно)
Формула расчета воздухообмена в час на основе CFM достаточно проста. Практически каждый может рассчитать это с помощью цифрового калькулятора.Все, что вам нужно знать, это площадь помещения, высота и CFM.
Это формула для ACH (воздухообмен в час):
ACH = CFM x 60 / (Площадь x Высота)
, где «Area» — это площадь помещения, в котором вы собираетесь установить устройство HVAC, а «Height» — это высота потолка.
Формула: «сколько кубических футов воздуха может обеспечить блок HVAC каждый час», деленное на объем помещения.
Мы всегда получаем CFM, но это объем воздуха в минуту .Чтобы рассчитать воздухообмен в час , мы должны перевести это в часы. Следовательно, умножение на 60 в приведенном выше уравнении.
Объем помещения рассчитывается как длина * ширина * высота . Умножив длину комнаты на ее ширину, мы получим площадь поверхности («Площадь»). Чтобы получить объем, нам нужно умножить площадь на высоту.
Сколько производителей очистителей воздуха ACH используют
Расчет рекомендуемой зоны охвата в технических характеристиках очистителя воздуха основан на рейтинге CADR, максимальном расходе воздуха и ACH.
По сути, для расчета рекомендуемой зоны охвата разные компании по очистке воздуха используют 1-5 воздухообменов в час. Те, которые используют 5 ACH, очень тщательно удаляют загрязнители воздуха, превышающие рекомендуемый размер комнаты, используя на 2 ACH меньше.
Вот список того, сколько ACH различных производителей воздухоочистителей обычно используют для расчета рекомендуемой зоны охвата:
- Alen BreatheSmart использует 2 ACH. Пример: Alen BreatheSmart 75i — очиститель воздуха №1 — имеет рекомендуемую зону охвата 1300 кв. Футов.Его максимальный воздушный поток составляет 350 кубических футов в минуту. При 5 ACH рекомендуемая зона покрытия составляет 520 кв. Футов.
- Очистители воздуха Coway рассчитаны на 2 или 5 кондиционеров. Пример: Big Airmega 400 имеет зону покрытия 1560 кв. Футов с рейтингом 350 CADR (2 ACH). Высокопроизводительный Coway AP-1512HH имеет зону покрытия 361 кв. Футов с рейтингом 246 CADR (5 ACH).
- Molekule имеет рекомендованную зону покрытия, но не предоставляет данных по ACH, CADR или максимальному расходу воздуха. Например, Molekule Air имеет зону покрытия 600 кв. Футов, но невозможно определить, сколько воздухообменов он производит в час.
- Honeywell использует 5 ACH. Пример: Honeywell HPA300 имеет зону покрытия 465 кв. Футов с рейтингом 300 CADR (5 ACH).
- Воздухоочистители Levoit интересны; они используют 3.33 ACH со своей лучшей моделью. Пример: Levoit LV-h235 имеет зону покрытия 463 кв.м и рейтинг CADR 360. Воздух меняют каждые 18 минут; Таким образом, установка Levoit производит 3,33 воздухообмена в час.
- Okaysou использует 3 воздухообмена в час. Пример: их самый популярный очиститель воздуха Okaysou AirMax8L имеет площадь покрытия 500 кв. Футов с рейтингом 210 CADR (3 ACH).
- Дайсон очень стесняется раскрывать размеры комнаты. Вот почему невозможно рассчитать ACH для любого очистителя воздуха Dyson.
Из всех устройств HVAC очистители воздуха уникальны в том, что касается ACH, потому что их работа наиболее точно соответствует спецификации ACH. По сути, ACH — второй по величине определяющий фактор, который указывает, насколько хорошо очистители воздуха очищают воздух.
Важно понимать, что расчет ACH составляет торжественно на основе расхода воздуха .Это не показатель того, насколько хорошо работает система фильтрации очистителя воздуха; он не измеряет эффективность фильтров HEPA, фильтров с активированным углем или даже фильтров генератора озона. Например, высокий ACH не снижает напрямую вероятность роста плесени (осмотр и тестирование плесени могут подтвердить это).
Существует еще одна более точная спецификация, действующая для очистителей воздуха, которая измеряет эффективность системы фильтрации; рейтинг CADR. Рейтинг CADR пропорционален как ACH, так и различным фильтрам, которые может использовать очиститель воздуха.По этой причине расчет ACH и последующий расчет CADR наиболее подходят для очистителей воздуха.
Чтобы рассчитать размер помещения на основе расхода воздуха (в кубических футах в минуту), вы должны использовать здесь калькулятор кубических футов в минуту.
Если у вас есть какие-либо вопросы относительно расчета воздухообмена в час, вы можете задать их нам в комментариях ниже.
Калькулятор длины, ширины и высоты к объему
Нажмите «Сохранить настройки», чтобы перезагрузить страницу с уникальным адресом веб-страницы для создания закладок и обмена текущими настройками инструмента.
✕ очистить настройки
Инструмент «Отразить» с текущими настройками и рассчитать длину, ширину или высоту
К сожалению, здесь не удалось отобразить графику, потому что ваш браузер не поддерживает холст HTML5.Сопутствующие инструменты
Руководство пользователя
Этот онлайн-инструмент вычисляет объем прямоугольной коробки, сплошного тела или пространства по длине, ширине и высоте. Нет необходимости вводить значения в одних и тех же единицах измерения, просто выберите желаемые единицы для каждого измерения и рассчитанного объема.
После ввода размеров длины, ширины и высоты рассчитанный объем отобразится в поле ответа. Также будет показано изображение масштабированного трехмерного чертежа с правильными пропорциями и помечено каждым размером и рассчитанным объемом.
Формула
Формула, используемая калькулятором для вычисления объема объекта прямоугольной формы:
В = Д · Ш · В
Символы
- V = Объем
- L = длина
- W = Ширина
- H = высота
Объемные размеры — длина, ширина и высота
Введите длину, ширину и высоту прямоугольной формы.
Для преобразования единиц измерения длины, ширины и высоты используются следующие коэффициенты преобразования единиц СИ в метрах (м):
SI Метрические единицы длины префикса
- йоктометр (мкм) — 1 x 10 -24 м
- зептометр (zm) — 1 x 10 -21 м
- аттометр (am) — 1 x 10 -18 м
- фемтометр (фм) — 1 x 10 -15 м
- пикометр (пм) — 1 x 10 -12 м
- нанометр (нм) — 1 x 10 -9 м
- микрометров (мкм) — 0.000001 м
- миллиметр (мм) — 0,001 м
- сантиметр (см) — 0,01 м
- дециметр (дм) — 0,1 м
- метр (м) — 1 м
- декаметр (плотина) — 10 м
- гектометров — 100 м
- километр (км) — 1000 м
- мегаметр (мм) — 1000000 м
- гигаметр (Gm) — 1 x 10 +9 м
- тераметр (Тм) — 1 x 10 +12 м
- петаметр (Pm) — 1 x 10 +15 м
- exametre (Em) — 1 x 10 +18 м
- зеттаметр (Zm) — 1 x 10 +21 м
- йоттаметр (Ym) — 1 x 10 +24 м
Британские и американские единицы длины
- тысячная дюйма (тыс.) — 0.0000254 кв.м.
- дюймов (дюйм) — 0,0254 м
- фут — 0,3048 м
- ярд — 0,9144 м
- миль (миль) — 1609,344 м
- морская миля (морская миля) — 1852 м
Астрономические единицы
- астрономическая единица (у.е.) — 149 597 870 700 м
- световых лет — 9,460,730,472,580,800 м
- парсек (шт) — 30,856,775,814,913,672,789… м
- килопарсек (кпк) — 3,08567758142789… x 10 +19 м
- мегапарсек (Мпк) — 3.08567758142789… x 10 +22 м
- гигапарсек (Гпк) — 3,08567758142789… x 10 +25 м
Расчет объема
Это объем прямоугольной формы, который соответствует размерам, указанным для длины, ширины и высоты. Объем рассчитывается путем умножения каждого измерения и последующего преобразования его в выбранные единицы измерения объема.
Следующие коэффициенты пересчета в кубических метрах (м³) используются для перевода вычисленного объема в различные единицы измерения объема:
Метрические единицы измерения объема
- кубический нанометр (куб. Нм) — 1 x 10 -27 м³
- кубических микрометров (куб мкм) — 1 x 10 -18 м³
- кубический миллиметр (куб мм) — 1 x 10 -9 м³
- кубический сантиметр (куб см) — 1 x 10 -6 м³
- миллилитр (мл) — 1 x 10 -6 м³
- чайная ложка (ч. Л., Метрическая) — 5 x 10 -6 м³
- столовая ложка (столовая, метрическая) — 1.5 x 10 -5 м³
- стакан (метрический) — 2,5 x 10 -4 м³
- литр (л) — 1 x 10 -3 м³
- куб.м — 1 м³
- килолитр (kL) — 1 м³
- мегалитр (ML) — 1000 м³
- кубический километр (куб км) — 1 x 10 +9 м³
Английские имперские единицы измерения объема
- тыс. Куб. (Тыс. Куб.) — 1,6387064 x 10 -14 м³
- кубических дюймов (у.е.) — 1,6387064 x 10 -5 м³
- жидких унций (жидких унций, английская система мер) — 2.84130625 x 10 -5 м³
- пинта (пинта, дюймовая) — 5,68 26125 x 10 -4 м³
- галлонов (галлоны) — 4,54609 x 10 -3 м³
- кубических футов — 0,028316846592 м³
- кубический ярд (cu yd) — 0,764554857984 м³
- кубических миль — 4168181825,440579584 м³
- кубическая морская миля (cu nmi) — 6352182208 м³
Единицы измерения объема в США
- тыс. Куб. (Тыс. Куб.) — 1,6387064 x 10 -14 м³
- чайная ложка (ч. Л., Сша) — 4.928 375 x 10 -6 м³
- столовая ложка (Tbsp, usa) — 1.478676478125 x 10 -5 м³
- кубических дюймов (у.е.) — 1,6387064 x 10 -5 м³
- жидких унций (жидких унций, сша) — 2,95735295625 x 10 -5 м³
- чашка (США) — 2.365882365 x 10 -4 м³
- пинта (pt, usa liquid) — 4,73176473 x 10 -4 м³
- галлонов (галлон, жидкость США) — 3,785411784 x 10 -3 м³
- кубических футов — 0.028316846592 м³
- баррель (барр., Нефть) — 0,158987294928 м³
- кубический ярд (cu yd) — 0,764554857984 м³
- кубических миль — 4168181825,440579584 м³
- кубическая морская миля (cu nmi) — 6352182208 м³
Литры Метрическая префикс Единицы измерения объема
- йоктолитр (yL) — 1 x 10 -27 м³
- зептолитр (zL) — 1 x 10 -24 м³
- аттолитр (al) — 1 x 10 -21 м³
- фемтолитр (фл) — 1 x 10 -18 м³
- пиколитр (PL) — 1 x 10 -15 м³
- нанолитров (кв.нл) — 1 x 10 -12 м³
- микролитр (кв мкл) — 1 x 10 -9 м³
- миллилитр (кв. Мл) — 0.000001 м³
- сантилитр (кв.кл) — 0,00001 м³
- децилитр (дл) — 0,0001 м³
- литр (кв. Л) — 0,001 м²
- декалитр (дал) — 0,01 м³
- гектолитр (гл) — 0,1 м³
- килолитр (кв.кл) — 1 м³
- мегалитр (ML) — 1000 м³
- гигалитр (GL) — 1000000 м³
- тералитр (TL) — 1 x 10 +9 м³
- петалитр (PL) — 1 x 10 +12 м³
- exalitre (EL) — 1 x 10 +15 м³
- цетталитр (ZL) — 1 x 10 +18 м³
- йотталитр (YL) — 1 x 10 +21 м³
Кубические метры СИ Метрическая префикс Единицы измерения объема
- кубический йоктометр (куб.м) — 1 x 10 -72 м³
- кубический зептометр (куб.м) — 1 x 10 -63 м³
- кубический аттометр (куб. М3) — 1 x 10 -54 м³
- кубический фемтометр (куб фм) — 1 x 10 -45 м³
- кубический пикометр (куб.м.) — 1 x 10 -36 м³
- кубический нанометр (куб. Нм) — 1 x 10 -27 м³
- кубических микрометров (куб мкм) — 1 x 10 -18 м³
- кубический миллиметр (куб мм) — 1 x 10 -9 м³
- кубический сантиметр (куб см) — 0.000001 м³
- кубический дециметр (куб дм) — 0,001 м³
- куб.м — 1 м³
- кубических декаметров (куб. Дам) — 1000 м³
- кубический гектометр (куб.м.) — 1,000,000 м³
- кубический километр (куб км) — 1 x 10 +9 м³
- кубических мегамметров (куб.мм) — 1 x 10 +18 м³
- кубический гигаметр (куб.Гм) — 1 x 10 +27 м³
- кубический тераметр (куб.тм) — 1 x 10 +36 м³
- кубических петаметр (куб.м.) — 1 x 10 +45 м³
- кубический метр (куб.м.) — 1 x 10 +54 м³
- кубический зеттаметр (куб. М3) — 1 x 10 +63 м³
- кубический йоттаметр (куб.см) — 1 x 10 +72 м³
Кубические астрономические единицы
- кубическая астрономическая единица (у.е.) — 3.347928975810748964239359243 x 10 +33 м³
- кубических световых года (кубических световых года) — 8.4678666462371516595551248694562 x 10 +47 м³
- куб. Парсек (у.е. шт) — 2,937998946096347255544756436543… x 10 +49 м³
- кубических килопарсек (у.е. кпк) — 2,937998946096347255544756436543… x 10 +58 м³
- кубических мегапарсек (у.е. МПк) — 2,937998946096347255544756436543… x 10 +67 м³
- кубических гигапарсек (куб. Гигапарсек) — 2,937998946096347255544756436543… x 10 +76 м³
Приложения
Используйте этот калькулятор длины x ширины x высоты для определения объема в следующих приложениях:
- Объем отправляемой посылки для добавления в отгрузочные документы
- Объем гравия, необходимый для заполнения дорожки, автостоянки или проезжей части.
- Прямоугольный резервуар для хранения.
- Вместимость грузового отсека легкового, грузового автомобиля или фургона.
- Объем загрузки автомобиля для перемещения хранилища.
- Максимальный объем резервуара для воды.
- Сколько топлива требуется для заправки бака.
- Размер связки, необходимый для предотвращения утечек и разливов из контейнеров IBC.
- Количество мешков, необходимых для каждого материала для строительного проекта.
- Количество почвы, необходимое для заполнения ящика сеялки.
- Количество воды, необходимое для заполнения аквариума / аквариума.
- Наполнитель для пруда.
- Вместимость складского помещения из габаритов.
- IBC вместимость.
- Объем бассейна.
- Возможное место для багажа внутри чемодана.
- Цементная смесь, необходимая для заполнения фундаментов / опор.
- Объем кузова пикапа.
- Объем корпуса аудиодинамика.

 м.
м. м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м.


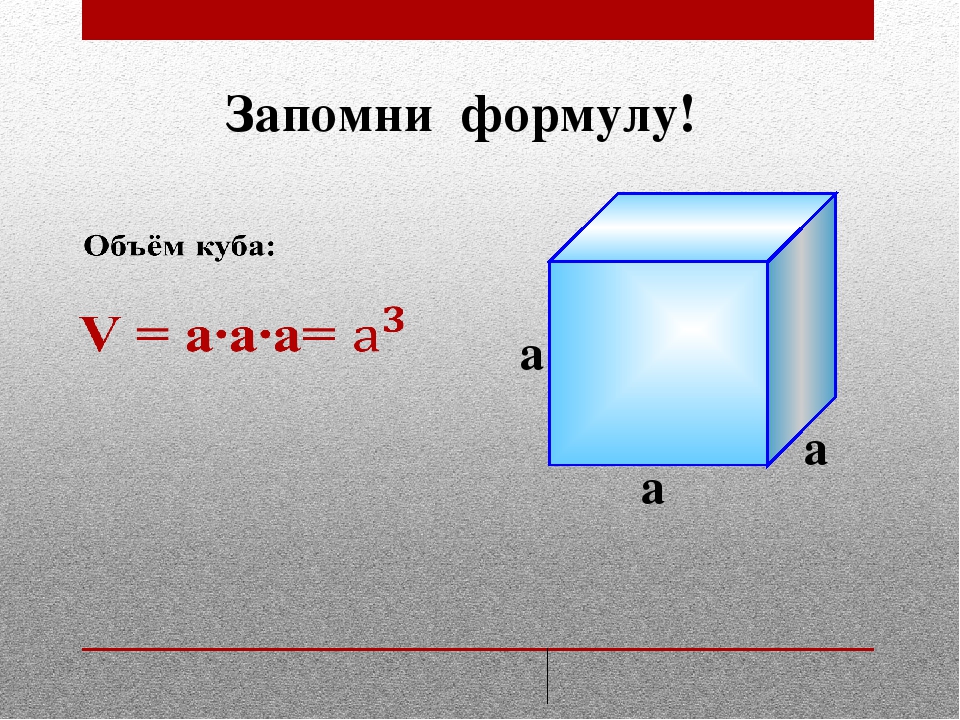


 Также для удобства в расчетах разработаны специальные компьютерные программы.
Также для удобства в расчетах разработаны специальные компьютерные программы.