Таблица умножения — Википедия
Табли́ца умноже́ния, она же табли́ца Пифаго́ра — таблица, где строки и столбцы озаглавлены множителями, а в ячейках таблицы находится их произведение. Используется для обучения школьников умножению.
Старейшая известная таблица умножения обнаружена в Древнем Вавилоне и имеет возраст примерно 4000 лет. Она основана на шестидесятеричной системе счисления[1]. Старейшая десятеричная таблица умножения найдена в Древнем Китае и датируется 305 годом до н. э.[1]
Иногда изобретение таблицы умножения приписывают Пифагору, в честь которого она названа в различных языках, включая французский, итальянский и русский[2].
В 493 году Викторий Аквитанский создал таблицу из 98 столбцов, которая представляла в римских числах результат перемножения чисел от 2 до 50[3].
В России первая таблица умножения была издана в 1682 году в первой печатной математической книге на русском языке, называвшейся «Считание удобное, которым всякий человек, купующий или продающий, зело удобно изыскати может число всякие вещи…» и содержавшей таблицу умножения пар чисел от 1×1 до 100×100, записанных славянскими цифрами
Джон Лесли в книге The Philosophy of Arithmetic (1820)[7] опубликовал таблицу умножения чисел до 99, позволявшую перемножать цифры парами. Он же рекомендовал ученикам заучивать таблицу умножения до 25.
В своё время введение заучиваемой наизусть таблицы умножения революционизировало устный и письменный счёт. До этого использовались разные хитрые способы вычисления произведений однозначных чисел, которые сильно замедляли весь процесс и служили источником дополнительных ошибок.
В российских школах значения традиционно доходят до 10×10. В Великобритании до 12×12, что связано в том числе с единицами английской системой мер длины (1 фут = 12 дюймов) и денежного обращения (существовавшей до 1971 г.: 1 фунт стерлингов = 20 шиллингам, 1 шиллинг = 12 пенсам).
В Советском Союзе таблицу умножения обычно «задавали на лето» после 1-го класса, а закрепляли на занятиях во 2-м классе (в возрасте 8 лет). В российских школах чаще всего проходят во 2-м классе. По стандартам английского школьного образования таблица умножения должна быть выучена к возрасту 11 лет (планируется ужесточение требования до 9 лет).[8]
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 | |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 | |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как найти результат по таблице умножения[править | править код]
Чтобы узнать результат произведения 4×8 по таблице умножения, нужно найти четвёрку в левом столбце и восьмёрку в верхней строке, провести от 4 горизонтальную линию и от 8 вертикальную. Клетка, на которой линии встречаются, является произведением (в данном случае 32).
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
Помимо широко известного применения классической таблицы умножения для выработки практических навыков умножения натуральных чисел, её можно использовать в некоторых математических доказательствах, например, при выводе формулы суммы кубов натуральных чисел или получении подобного выражения для суммы квадратов[9].
Наряду с таблицей умножения, в некоторых случаях бывают удобны таблицы сложения.
Таблица Кэли — в общей алгебре, таблица, которая описывает структуру конечных алгебраических систем с одной бинарной операцией. Названа в честь английского математика Артура Кэли. Имеет важное значение в дискретной математике, в частности, в теории групп, в которой в качестве операций рассматриваются умножение и сложение. Таблица позволяет определить, является ли группа абелевой, найти центр группы и обратные элементы по отношению к другим элементам в этой группе.
В высшей алгебре таблицы Кэли могут также использоваться для определения бинарных операций в полях, кольцах и других алгебраических структурах. Также они удобны при проведении действий в данных структурах.
Модулярная арифметика[править | править код]
Все остатки от деления на натуральное число образуют кольцо, а от деления на простое число — поле. Это иллюстрируется таблицами умножения:
Таблица умножения в кольце вычетов по модулю 8
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 0 | 2 | 4 | 6 | 0 | 2 | 4 | 6 |
| 3 | 0 | 3 | 6 | 1 | 4 | 7 | 2 | 5 |
| 4 | 0 | 4 | 0 | 4 | 0 | 4 | 0 | 4 |
| 5 | 0 | 5 | 2 | 7 | 4 | 1 | 6 | 3 |
| 6 | 0 | 6 | 4 | 2 | 0 | 6 | 4 | 2 |
| 7 | 0 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Таблица умножения в поле вычетов по модулю 5
| × | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
- ↑ 1 2 Jane Qiu. Ancient times table hidden in Chinese bamboo strips (англ.) // Nature : journal. — 2014. — 7 January. — DOI:10.1038/nature.2014.14482.
- ↑ Например, в Farrar, John. An Elementary Treatise on Arithmetic (англ.).
- ↑ Maher, David W.; Makowski, John F. Literary evidence for Roman arithmetic with fractions (англ.) // Classical Philology. — 2001. — No. 4 (96). — P. 383.
- ↑ Депман И. А. История арифметики. Пособие для учителей. — М.: Государственное учебно-педагогическое издательство Министерства Просвещения РСФСР, 1959. — С. 196—198. — 28 000 экз.
- ↑ Считание удобное : Таблица умножения — карточка электронного каталога РГБ
- ↑ Считание удобное : Таблица умножения — карточка каталога Научной библиотеки МГУ
- ↑ Leslie, John. The Philosophy of Arithmetic; Exhibiting a Progressive View of the Theory and Practice of Calculation, with Tables for the Multiplication of Numbers as Far as One Thousand (англ.). — Edinburgh: Abernethy & Walker, 1820.
- ↑ Children must learn times tables by age nine… // Daily Mail, 17.12.2011
- ↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Матезис, 1923. — С. 68—72.
Таблица умножения на 6, 7, 8 и 9 на пальцах
Если моя память мне не изменяет, таблица умножения до 5 включительно далась достаточно легко. Но вот с умножением на 6, 7, 8 и 9 возникали определенные трудности. Если бы я знала такой трюк раньше, домашнее задание выполнялось бы минимум в два раза быстрее 😉

©photo
Умножение на 6, 7 и 8
 таблица умножения на пальцах
таблица умножения на пальцахПоверните кисти ладонями к себе и присвойте каждому пальцу цифры от 6 и до 10 начиная с мизинца.

Теперь попробуем умножить, например, 7х8. Для этого соедините палец №7 на левой руке с пальцем №8 на правой.
 таблица умножения на пальцах
таблица умножения на пальцахА теперь считаем пальцы: количество пальцев под соединенными — это десятки.
 таблица умножения на пальцах
таблица умножения на пальцах(картинка кликабельна)
А пальцы левой руки, оставшиеся сверху, умножаем на пальцы правой — это и будут наши единицы (3х2=6). Итоге равен 56.
Иногда бывает так, что при умножении «единиц» результат получается больше 9. В таких случаях нужно плюсовать оба результата в столбик.
Например, 7х6. В этом случае получается, что «единицы» равны 12 (3х4). В десятки равны 3.
3 (десятки)
+
12 (единицы)
________
42
Умножение на 9
Снова поверните кисти ладонями к себе, но теперь нумерация пальцев будет идти по порядку с лева на право, то есть от 1 до 10.

Теперь умножаем, например, 2х9. Все то, что идет до пальца №2 — это десятки (то есть 1 в этом случае). А все то, что остается после пальца №2 — единицы (то есть 8). В итоге получаем 18.
Таблица умножения на 6
| Множители | Произведение (Результат) |
|---|---|
| 6 * 1 = | 6 |
| 6 * 2 = | 12 |
| 6 * 3 = | 18 |
| 6 * 4 = | 24 |
| 6 * 5 = | 30 |
| 6 * 6 = | 36 |
| 6 * 7 = | 42 |
| 6 * 8 = | 48 |
| 6 * 9 = | 54 |
| 6 * 10 = | 60 |
| 6 * 11 = | 66 |
| 6 * 12 = | 72 |
| 6 * 13 = | 78 |
| 6 * 14 = | 84 |
| 6 * 15 = | 90 |
| 6 * 16 = | 96 |
| 6 * 17 = | 102 |
| 6 * 18 = | 108 |
| 6 * 19 = | 114 |
| 6 * 20 = | 120 |
| 6 * 21 = | 126 |
| 6 * 22 = | 132 |
| 6 * 23 = | 138 |
| 6 * 24 = | 144 |
| 6 * 25 = | 150 |
| 6 * 26 = | 156 |
| 6 * 27 = | 162 |
| 6 * 28 = | 168 |
| 6 * 29 = | 174 |
| 6 * 30 = | 180 |
| 6 * 31 = | 186 |
| 6 * 32 = | 192 |
| 6 * 33 = | 198 |
| 6 * 34 = | 204 |
| 6 * 35 = | 210 |
| 6 * 36 = | 216 |
| 6 * 37 = | 222 |
| 6 * 38 = | 228 |
| 6 * 39 = | 234 |
| 6 * 40 = | 240 |
| 6 * 41 = | 246 |
| 6 * 42 = | 252 |
| 6 * 43 = | 258 |
| 6 * 44 = | 264 |
| 6 * 45 = | 270 |
| 6 * 46 = | 276 |
| 6 * 47 = | 282 |
| 6 * 48 = | 288 |
| 6 * 49 = | 294 |
| 6 * 50 = | 300 |
| 6 * 51 = | 306 |
| 6 * 52 = | 312 |
| 6 * 53 = | 318 |
| 6 * 54 = | 324 |
| 6 * 55 = | 330 |
| 6 * 56 = | 336 |
| 6 * 57 = | 342 |
| 6 * 58 = | 348 |
| 6 * 59 = | 354 |
| 6 * 60 = | 360 |
| 6 * 61 = | 366 |
| 6 * 62 = | 372 |
| 6 * 63 = | 378 |
| 6 * 64 = | 384 |
| 6 * 65 = | 390 |
| 6 * 66 = | 396 |
| 6 * 67 = | 402 |
| 6 * 68 = | 408 |
| 6 * 69 = | 414 |
| 6 * 70 = | 420 |
| 6 * 71 = | 426 |
| 6 * 72 = | 432 |
| 6 * 73 = | 438 |
| 6 * 74 = | 444 |
| 6 * 75 = | 450 |
| 6 * 76 = | 456 |
| 6 * 77 = | 462 |
| 6 * 78 = | 468 |
| 6 * 79 = | 474 |
| 6 * 80 = | 480 |
| 6 * 81 = | 486 |
| 6 * 82 = | 492 |
| 6 * 83 = | 498 |
| 6 * 84 = | 504 |
| 6 * 85 = | 510 |
| 6 * 86 = | 516 |
| 6 * 87 = | 522 |
| 6 * 88 = | 528 |
| 6 * 89 = | 534 |
| 6 * 90 = | 540 |
| 6 * 91 = | 546 |
| 6 * 92 = | 552 |
| 6 * 93 = | 558 |
| 6 * 94 = | 564 |
| 6 * 95 = | 570 |
| 6 * 96 = | 576 |
| 6 * 97 = | 582 |
| 6 * 98 = | 588 |
| 6 * 99 = | 594 |
| 6 * 100 = | 600 |
| … * 101 = | … |
Автор: Bill4iam
Таблица умножения и игра, чтобы быстро выучить
С лучшей бесплатной игрой таблица умножения учится очень быстро. Проверьте это сами!
Учить таблицу умножения — игра
Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.
Таблица умножения – таблица, где строки и столбцы озаглавлены множителями (1, 2, 3, 4, 5…), а ячейки таблицы содержат их произведение. Применяется таблица для обучения умножению. Здесь есть игра и картинка для печати. Для скачивания игры с таблицей на компьютер, сохраните страницу (Ctrl+S). Также посмотрите таблицу деления.
Смотрите ниже шпаргалки в полной форме.
Распечатать таблицу умножения
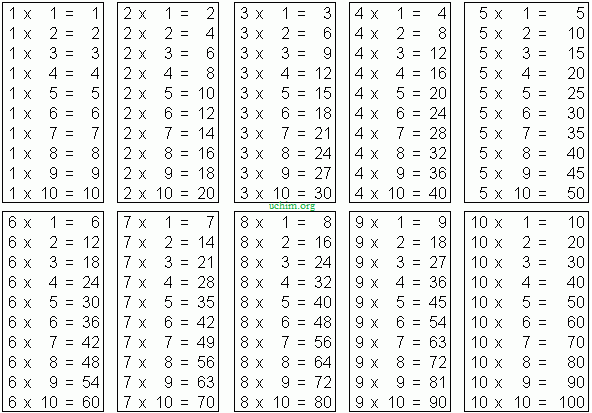
Умножение прямо на сайте (онлайн)
*https://uchim.org/matematika/tablica-umnozheniya — uchim.org
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как умножать числа столбиком (видео по математике)
Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.
Нужно распечатать таблицу умножения? Просто нажмите на ссылку печать таблицы умножения. Либо скопируйте картинку (первая таблица) в Ворд (Microsoft Office Word) и распечатайте с помощью сочетания клавиш Ctrl+P. Смотрите также таблицу квадратов.
Всё для учебы » Математика в школе » Таблица умножения и игра, чтобы быстро выучить
Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):
Умножение числа 6. Умножение на 6 — урок. Математика, 3 класс.
Умножение числа \(6\)
На каждой картинке по \(6\) пуговиц. Всего \(9\) картинок.
Сложение одинаковых слагаемых \(6\) можно заменить умножением на \(2\), на \(3\), на \(4\), на \(5\), \(6\), \(7\), \(8\), \(9\).
\(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
\(6\) | \(12\) | \(18\) | \(24 \) | \(30\) |
\(6\) | \(7\) | \(8\) | \(9\) |
\(36\) | \(42\) | \(48\) | \(54\) |
\(6· 2 =12\). Шестью два — двенадцать.
\(6· 3 = 18\). Шестью три — восемнадцать.
\(6· 4 =24\). Шестью четыре — двадцать четыре.
\(6· 5 = 30\). Шестью пять — тридцать.
\(6· 6 = 36\). Шестью шесть — тридцать шесть.
\(6· 7 =42\). Шестью семь — сорок два.
\( 6· 8 = 48\). Шестью восемь — сорок восемь.
\(6· 9 =54\). Шестью девять — пятьдесят четыре.
Умножение на \(6\)
Поменяв местами множители, получим:
\(2 · 6 = 12\),
\(3 · 6 = 18\),
\(4 · 6 = 24\),
\(5 · 6 = 30\),
\(6 · 6 = 36\),
\(7 · 6 = 42\),
\(8 · 6 = 48\),
\(9 · 6 = 54\).
Как научить детей таблице умножения один раз и на всю жизнь

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Таблица умножения — базовое понятие в математике, с которым мы знакомимся еще в начальной школе и которое потом используем всю жизнь вне зависимости от профессии. Вот только дети не спешат заучивать бесконечные столбики наизусть, особенно если задание пришлось на каникулы.
AdMe.ru даст советы, как легко выучить таблицу вместе с детьми и сделать этот процесс увлекательным.
Таблица Пифагора

Несмотря на то что задача — выучить, то есть заучить, таблицу наизусть, прежде всего важно понять суть самого действия. Для этого можно заменить умножение сложением: одинаковые числа складываются столько раз, на сколько мы умножаем. Например, 6×8 — это сложить 8 раз по 6.
Выделяем цветом одинаковые значения

Отличным помощником для изучения умножения станет таблица Пифагора, которая также демонстрирует некоторые закономерности. Например то, что от перемены мест множителей произведение не меняется: 4×6 = 6×4. Отметьте такие «зеркальные» ответы определенным цветом — это поможет запомнить и не запутаться при повторении.

Начинать изучение таблицы Пифагора лучше с самых простых и понятных частей: умножения на 1, 2, 5 и 10. При умножении на единицу число остается неизменным, а умножение на 2 дает нам удвоенное значение. Все ответы умножения на 5 оканчиваются либо на 0, либо на 5. А вот умножив на 10, в ответе мы получим двузначное число из цифры, которую умножали, и нуля.
Таблица для закрепления результата

Для закрепления результатов нарисуйте с ребенком пустую таблицу Пифагора и предложите ему заполнить клеточки правильными ответами. Для этого вам понадобится всего лишь листок бумаги, карандаш и линейка. Нужно нарисовать квадрат и поделить его на 10 частей по вертикали и горизонтали. А затем заполнить верхнюю строчку и крайний левый столбик числами от 1 до 9, пропустив первую клетку.
Конечно, все дети индивидуальны и универсального рецепта не существует. Главная задача родителя — найти подход и поддержать свое чадо, ведь все мы когда-то начинали с таких одновременно простых и сложных шагов.
2. Таблица умножения на 9. Нахождение частного по таблице умножения
\(·\) | \(2\)
| \(3\)
| \(4\)
| \(5\)
| \(6\)
| \(7\)
| \(8\)
| \(9\) ↓ |
\(2\) | \( \) | \( \) | \( \) | \( \) | \( \) | \( \) | \(18\) | |
\(3\) | \( \) | \( \) | \( \) | \( \) | \( \) | \(27\) | ||
\(4\) | \( \) | \( \) | \( \) |
|
| \(36\) | ||
\(5\) | \( \) |
| \(45\) | |||||
\(6\) | \( \) | \( \) |
| \(54\) | ||||
\(7\) | \( \) |
|
| \(63\) | ||||
\(8\) | \( \) |
| \(72\) | |||||
\(9\)→ | \(18\) | \(27\) | \(36\) | \(45\) | \(54\) | \(63\) |
Множители можно менять местами.
2⋅9=9⋅2=18,3⋅9=9⋅3=27,4⋅9=9⋅4=36,5⋅9=9⋅5=45,6⋅9=9⋅6=54,7⋅9=9⋅7=63,8⋅9=9⋅8=72,9⋅9=81.
По таблице умножения можно найти значение частного.
Например, найдём частное \(72 : 9\). Частное связано с примером на умножение \(9\) \(·\) \(?\) \(=\) \(72\).
В строке с первым числом \(9\) найдём число \(72\), которое находится в столбце с первым числом \(8\).
Значит, \(9· 8 = 72\). Следовательно, \(72 : 9=8\).
