Уклон 1 6 это сколько: Уклон 1 6 сколько это

Содержание

Уклон 1 6 сколько это

Адаптация пандусов для МГН

В соответствии с приказом Минстроя России №750/пр от 21 октября 2015 г. «Об утверждении изменений №1 к СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» «При проектировании реконструируемых, подлежащих капитальному ремонту и приспосабливаемых существующих зданий и сооружений уклон пандуса принимается в интервале от 1:20 (5%) до 1:12 (8%)».

Соотношение	Проценты	Градусы
1:20	5%	2,9°
1:12	8%	4,8°
1:10	10%	5,7°

Введите параметры будущего пандуса, исходя из данных объекта. Параметры необходимо вводить в милиметрах. Нажмите кнопку «рассчитать». Длина наклонной площадки в рассчитывается в милиметрах. Также Вы получите рекомендации относительно параметров, которые у Вас получились.

Основным действующим нормативным документом для определения уклона пандуса и его длины в РФ является СП 59.

13330.2012 «Доступность зданий и сооружений для маломобильных групп населения»

При высоте марша до 800 мм — мах угол 2,86° При высоте марша до 200 мм — мах угол 5,71° Для временных конструкций при высоте марша до 800 мм — мах угол 4,76°

Пандус – это устройство для адаптации социально-значимых объектов и открытых пространств: вход в здание, сопровождение лестницы, пешеходный переход и т.д. Пандус необходим, чтобы сделать жизнь маломобильных групп населения комфортнее: пожилые люди, с коляской или тяжелой поклажей, с костылями после травм, инвалиды-колясочники.

Активное развитие и продвижение федеральной программы «Доступная среда» сподвигло многие организации установить пандусы на входной группе. Однако зачастую это делается либо для галочки, либо организациями, не владеющими навыками и знаниями существующих нормативов. Поэтому не всегда готовое изделие соответствует государственным стандартам. Как результат — недоступность для людей с ограничениями.

Нормативы для пандусов 2018

По нормативам СП 59. 13330.2016 (с учетом вступивших в силу изменений 15 Мая 2017 года) пандус должен иметь следующие характеристики:

Список документации, рекомендуемой к ознакомлению:

СНиП 35-01-2001 содержит предписания по адаптации жилых домов и социально-значимых объектов для маломобильных групп населения. А так же конкретные ограничения по установке и параметрам пандусов. ГОСТ Р 51261-99 содержит технические требования к стационарным опорным устройствам. СП 30-102-99 содержит требования к входной площадке. СП 59.13330.2012 содержит предписания по доступности зданий и сооружений для маломобильных групп населения

Угол наклона пандуса не должен превышать уклон в отношении 1:20 (5%). В данном случае очень часто проценты путают с градусами. В результате чего подъем /спуск получается в разы выше. Угол наклона — это соотношение длины к высоте подъема.

Справка! В ряде некоторых случаев допускается небольшое увеличение угла наклона пандуса:

При временном сооружении пандуса (ремонте или реконструкции здания). Если его высота не превышает 0,5 м, а промежуток между площадками не более 6 м, уклон может быть 8% или 1:12
Если высота подъема не достигает 0,2 м, уклон допустим в пропорции 1:10 (10%).
Длина непрерывного движения марша пандуса не должна превышать 9,0 м, далее необходимо организовывать разворотную площадку или площадку отдыха.
Длина горизонтальной площадки прямого пандуса должна быть не менее 1,5 м.
Пандусы должны иметь двухстороннее ограждение с поручнями на высоте 0,9 и 0,7 м.
Поверхность пандуса должна быть нескользкой текстурой.
Поверхность марша пандуса должна визуально контрастировать с горизонтальной поверхностью в начале и конце пандуса.

Запомните! При перепаде высоты от трех метров, вместо пандусов применяются подъемные устройства. В данном случае наличие пандуса будет бесполезным и недоступным для инвалида-колясочника.

Поручни для пандуса

— В начале и конце поручни должны быть длиннее на 300 мм и иметь закруглённую форму.

— Верхний поручень расположен на высоте 900 мм.

— Расстояние между поручнями 900-1000 мм.

— Перила должны быть круглого сечения с диаметром от 30 до 50 мм.

— Начало и конец маркируются предупредительными полосами.

— Нижний поручень должен быть на расстоянии 700 мм.

— При высоте пандуса более 0,45 м необходимо наличие бортиков высотой не менее 0,05 м.

— Покрытие пандуса должно обладать противоскользящим эффектом.

— Минимальное расстояние от гладкой стены 45 мм, от неровной 60 мм.

— Поручни с внутренней стороны не должны прерываться.

— Поручни изготавливаются из металла и устанавливаются с обеих сторон наклонной площадки.

Если пандус изначально соответствует всем строительным параметрам, то его можно оснастить необходимыми дополнительными устройствами при их отсутствии:

Опорными поручнями. Расстояние между поручнями пандуса одностороннего движения должно быть в пределах 0,9-1,0 м, чтобы инвалид-колясочник мог на них подтянуться. Также для удобства и безопасности хвата поручни должны иметь закругленную форму и выступать на 300 мм от края.
Контрастной тактильной разметкой (для незрячих и слабовидящих людей). Разметкой следует обозначать сами поручни и подстилающую поверхность. С внутренней стороны поручней можно приклеить тактильные наклейки для обозначения начала и конца препятствия.

Если пандус изначально не соответствует конструкторским параметрам в соответствии со сводами правил, то его следует демонтировать, а на его месте организовать доступный пандус.

ВОПРОСЫ ПО АДАПТАЦИИ АВТОПАРКОВКА ДЛЯ МГН АДАПТАЦИЯ ТРОТУАРОВ ДЛЯ НЕЗРЯЧИХ АДАПТАЦИЯ ЛЕСТНИЦ ДЛЯ МГН АДАПТАЦИЯ ВХОДНОЙ ГРУППЫ АДАПТАЦИЯ ХОЛЛА В ПОМЕЩЕНИИ АДАПТАЦИЯ САНУЗЕЛА ДЛЯ НЕЗРЯЧИХ АДАПТАЦИЯ ЛИФТОВ ДЛЯ МГН

НАШЕ ПРЕИМУЩЕСТВО — ДОЛГОЛЕТНИЙ ОПЫТ и КАЧЕСТВО!

Уклон и Конусность

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения. Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах. Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.

Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

Как рассчитать уклон пандуса

Как начертить уклоны и конусность

Во многих деталях машин используются уклоны и конусность. Уклоны встречаются в профилях прокатной стали, в крановых рельсах, в косых шайбах и т. д. Конусности встречаются в центрах бабок токарных и других станков, на концах валов и ряда других деталей.

Уклон характеризует отклонение прямой линии от горизонтального или вертикального направлений. Для того чтобы построить уклон 1:1, на сторонах прямого угла откладывают произвольные, но равные величины (рис. 1). Очевидно, что уклон 1:1 соответствует углу в 45 градусов. Чтобы построить линию с уклоном 1:2, по горизонтали откладывают две единицы, для уклона 1:3 — три единицы и т. д. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а. Величину уклона на чертеже в соответствии с ГОСТ 2.307—68 указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть горизонтальна, другая — наклонена примерно под углом 30° в ту же сторону, как и сама линия уклона.

На рисунке в качестве примера построен профиль несимметричного двутавра, правая полка которого имеет уклон 1:16. Для ее построения находят точку А с помощью заданных размеров 26 и 10. В стороне строят линию с уклоном 1:16, для чего по вертикали откладывают, например, 5 мм, а по горизонтали 80 мм; проводят гипотенузу, направление которой определяет искомый уклон. С помощью рейсшины и угольника через точку А проводят линию уклона, параллельную гипотенузе.

Конусностью называют отношение диаметра основания конуса к его высоте. В этом случае конусность К=d/l. Для усеченного конуса К = (d-d1)/l. Пусть требуется построить конический конец вала по заданным размерам: d — диаметр вала — 25 мм; I — общая длина конца вала — 60 мм; l1 — длина конической части — 42 мм; d1 — наружный диаметр резьбы — 16 мм; К — конусность 1 : 10 (рис. 3, б). Прежде всего, пользуясь осевой, строят цилиндрическую часть вала, имеющую диаметр 25 мм. Этот размер определяет также большее основание конической части. После этого строят конусность 1:10. Для этого строят конус с основанием, равным 10 мм, и высотой, равной 100 мм (можно было бы воспользоваться и размером 25 мм, но в этом случае высота конуса должна быть взята равной 250 мм, что не совсем удобно).

Калькулятор расчета пандуса

Параллельно линиям найденной конусности проводят образующие конической части вала и ограничивают ее длину размером 42 мм. Как видно, размер меньшего основания конуса получается в результате построения. Этот размер обычно не наносят на чертеж. Запись М16X1,5 является условным обозначением метрической резьбы, о чем подробнее будет сказано дальше.

TBegin—>TEnd—>

Рис. 1. Построение уклонов

Перед размерным числом, характеризующим конусность, наносят условный знак в виде равнобедренного треугольника, вершину которого направляют в сторону вершины самого конуса. Знак конусности располагают параллельно оси конуса над осью или на полке линии-выноски, заканчивающейся стрелкой, как в случае надписи уклона. Конусность выбирают в соответствии с ГОСТ 8593—57 .

Рис. 2. Пример построения уклонов

TBegin—>TEnd—>

Рис. 3. Построение конусности

Пандусы для инвалидов

Пандус – это наклонная площадка, соединяющая две горизонтальные плоскости, расположенные на разной высоте. Такая конструкция устанавливается с целью обеспечения беспрепятственного перемещения инвалидных колясок и других колесных механизмов с одного уровня на другой.

Пандусы бывают следующих видов:

Стационарные — размещаются у входов в помещения,устанавливаются на длительный сроки изготавливаются индивидуально, с учетом всех особенностей места их монтажа. Конструкции такого типа бывают одно- и двухпролетные.
Откидные -складывающиеся конструкции для инвалидов , которые устанавливают в тех местах, где пространство несколько ограничено. При необходимости конструкцию можно сложить и отодвинуть, чтобы она не загораживала основной проход. При этом изделие фиксируется на стене или перилах с помощью специальных приспособлений.
Съемные – это рампы, раздвижные и телескопические пандусы, а также роллпандусы (имеют сравнительно малые размеры и могут скручиваться,как коврик).

Они достаточно удобны, благодаря своей компактности и мобильности.

Пандусы изготавливаются в соответствии с нормами проектирования — СНиП 35-01-2001; СП 59.13330.2012; ГОСТ Р 51261-99

1. Размеры

Перед подъемом и в конце спуска инвалидного пандуса обязательно должны присутствовать площадки, размеры которых должны превышать габариты инвалидной коляски.
При сооружении конструкции на лестнице с двумя и более пролетами, монтируются промежуточные площадки, позволяющие развернуть инвалидную коляску. Размеры такой площадки : ширина в два раза превышает ширину марша, а глубина — минимум 150 сантиметров.
Ширина конструкции, если на ней предусмотрено одностороннее движение инвалидов составляет минимум 900 мм, а с двухсторонним движением – 1800мм. Во втором случае угол наклона уменьшается до 6.7%. Возможен также вариант с установкой поручня посредине конструкции.

2. Угол наклона пандуса для инвалидных и детских колясок

Уклон пандуса — одна из важнейших его характеристик, т. к. если наклонные поверхности пандуса выполнены с уклоном, превышающим нормы, тоего использование небезопасно как для инвалидов, так и для родителей с детскими колясками. Величина допустимого уклона пандуса регламентируется СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» — актуализированная версия СНиП 35-01-2001 (документ введен в действие 01.01.2013).

Нормативный угол наклона пандуса для колясок должен быть не более 1:20 (5% или 2,86 градусов) и длина одного марша пандуса не более 8 м. В ряде случаев допускается увеличение максимального уклона пандуса:

до 1:12 (8% или 4,76 градуса) — для временных сооружений и объектов инфраструктуры, при условии, что перепад высот между горизонтальными площадками менее 0,5 м и длина одного марша пандуса не более 6,0 м;
до 1:10 (10% или 5,71 градуса) — при перепаде высот полов менее 0,2 м.

Как рассчитать угол наклона пандуса?

1 способ.

Наклон пандуса = H (перепад высот, который необходимо оборудовать пандусом) / L (длина горизонтальной проекции наклонного участка пандуса).

Например, для того, чтобы рассчитать пандус для входа в здание, высота крыльца которого составляет 0,4 м, необходимо использовать соотношение 1:12.

Расчет угла наклона пандуса

Составляем простую пропорцию L=12*0.4 м = 4,8 м. Вычисляем длину наклонной поверхности пандуса = корень квадратный из (4,82+ 0,42) = 4,8 м.В результате расчётов мы видим, что такой пандус может быть устроен без горизонтальных площадок, так как длина его наклонных поверхностей менее 6 м.

Наклон пандуса может быть выражен в градусах, процентах и в виде отношения высоты к длине:

Единицы измерения уклона пандуса

Норматив

Соотношение

Значение в %

Значение в градусах

стандартный по СП 59.13330.2012	5%	2,86 градуса
для временных сооружений	8%	4,76 градуса
при перепаде высот до 0,2 м	10%	5,71 градуса

2 способ.

Уклон пандуса определяется СНиП 35-01-2001 и СП 59.13330.2012

В обозначенных выше документах есть разночтения по стандартной величине уклона пандусов. В СНиП 35-01-2001 допустимый уклон пандуса составляет1:12 (или 8%), а по СП 59.13330.2012 — 1:20 (или 5%).

Учитывая, что СНиП 35-01-2001 является национальным стандартом, утвержденным Распоряжением Правительства РФ от 21 июня 2010г. № 1047-р, а также, если заказчиком не выдвигается требование спроектировать пандус по СП 59.13330.2012,возможно проектирование и изготовление пандусов по нормативам, обозначенным в СНиП 35-01-2001, т.е.: допустимый уклон пандуса — 1:12 (или 8%, или 4,76 градуса).

Высота порога (м) * 100

Длина пандуса (м) = ——————————

% уклона

Уклон и Конусность

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон.

Как рассчитать пандус?

Уклон это отклонение прямой линии от вертикального или горизонтального положения. Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

Установка пандусов для маломобильных групп.

Новый уклон пандуса для инвалидов — очень мал!

Уточняйте цену.

Установка пандусов для маломобильных групп

Первое на что стоит обратить внимание при установки пандуса — это его уклон. Уклон является важнейшей характеристикой во время установки, если во время установки пандуса допустить ошибку либо уход от нормы — использование такого пандуса буден не безопасно для самого инвалида. Нормативные акты, которые регламентируют угол наклона СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» — актуализированная версия СНиП 35-01-2001, документ введен в действие 01.01.2013..

В акте точно сказано, что нормативный угол наклона для пандусов и колясок должен быть 1:20 в процентном отношение это 5 процентов или примерно 2,86 градуса. Также допускаются некоторые расхождение так: До 1:12 т.е 8% или 4,76 градуса — для возведение временных сооружений и объектов производственной инфраструктуры, обязательным условием возведение является горизонтальная площадка не менее 0,5 метров, в купе с соотношением одного марша пандуса не более 6 метров. до 1:10 т.е 10% или 5,71 градуса — при минимальных перепадов высот менее 0,2 метра.

Как рассчитать угол наклона пандуса?

На данный вопрос существует точный и однозначный ответ. Формула: наклон пандуса = H / L. По данной формуле, где H = перепад высот, который необходимо оборудовать пандусом, а L — длина горизонтальной проекции наклонного участка пандуса.

Уклон пандуса для инвалидов. Пример расчетов для, к примеру, поставлена задача, рассчитать пандус для входа в здание. Высота крыльца = 0,4м. Необходимое соотношение 1:12, составляем пропорцию L=12*0.4 м = 4,8 м. Вычисляем длину наклонной поверхности пандуса = корень квадратный из (4,82+ 0,42) = 4,8 м Пандус может быть устроен без горизонтальных площадок, так как длина его наклонных поверхностей менее 6 м. Если говорить об единицах измерение, которое мы используем при работе, то накол чаще всего выражен в градусах, также в процентах, и в виде отношений высоты к длине.

Если говорить о единицах измерения, то наклон пандуса может быть выражен в градусах, процентах и в виде отношения высоты к длине. В тех документах, которые были в начале статьи законодатель допустил разночтение, а именно, по стандартному углу наклона пандусов для инвалидов в документе СНиП 35-01-2001, указано, что возможен уклон 1:12 либо 8%, в то время как в другом документе СП 59.13330.2012 — он равен 1:20 (или 5%). При возможных колизии с законом, учитывается СНиП 35-01-2001, так как данный документ является Распоряжением Правительства РФ от 21 июня 2010 г. № 1047-р.

Если у вас остались вопросы Мы всегда на них сможем ответит по телефону, который указан на сайте.

Предлагаем пандус для маломобильных групп по нормам СНиП и ГОСТ, оборудование для инвалидов и пандус для маломобильных групп от производителя, заказ и установка в Москве и по России. Обращайтесь

Как рассчитать угол уклона и длину пандуса?

Расчет уклона пандуса для инвалидов

Согласно нормативно-правовым нормам Российской Федерации ответственность за установку пандуса для инвалидов несет владелец помещения/здания. За неисполнение требований СНиП, ГОСТ и СП предусматриваются санкции (ст. 13 Кодекса об административных правонарушениях) в виде штрафа или временного приостановления административной деятельности. Пандус должен быть безопасным, надежным и соответствовать нормам по ширине, углу наклона, наличию поручней и пр.

Каким должен быть уклон пандуса

Угол наклона пандуса должен соответствовать определенным нормам для удобства инвалидов-колясочников. Если инвалид не замечает уклона, и передвигается по пандусу легко, то с пандусом все в порядке. Согласно Своду правил 59.13330.2012, при монтаже пандуса следует учитывать следующие нюансы:

Установка пандуса обязательна, если перепад высот между поверхностями, которые должен преодолеть инвалид, более 4 см.
Уровень уклона пандуса зависит от его минимальной высоты и длины. Чем больше высота, на которую заезжает колясочник, тем длиннее будет пандус.
Уклон не должен превышать 8% (4,8 градуса) при установке временного пандуса с высотой до 50 см и 5% (2,9 градуса) на каждые 80 см длины при установке стационарного пандуса (высота может быть больше 50 см).
Пандус нельзя установить сразу на определенной высоте.
В начале и в конце конструкции, а также каждые 8-9 м пандуса должна быть ровная площадка для отдыха и/или разворота.
Поверхность пандуса шириной 1 м должна быть покрыта противоскользящими материалами и иметь по краям бортики высотой 5 см.

Формула вычисления угла наклона и длины пандуса

Чтобы рассчитать правильный угол установки пандуса и его длину, соответствующую нормам, используются следующие формулы:

Для вычисления нужной длины:1 (единица) / угол наклона*высота подъема. Например, при нормативном значении угла 5% и высоте 80 см мы получаем 1/5*80=16, то есть длину 16 м.
Для вычисления правильного угла: высота подъема в см/длина пандуса (предполагаемая) в м. Например, высота поверхности, на которую должен попасть инвалид, составляет 1 м (100 см), и вы предполагаете, что пандуса длиной 12 м должно хватить. Вычисляем: 100/12=8,3. 8,3% — недопустимый уклон пандуса.

Если у вас возникли вопросы по поводу расчета уклона пандуса или его установки, звоните в компанию «ММС», сотрудники которой окажут профессиональную помощь. Наш номер 8 800 301-15-21.

Возврат к списку

Пандусы для маломобильных групп населения наклонные -Полезная информация

Уклон пандуса — одна из важнейших его характеристик — если наклонные поверхности пандуса выполнены с уклоном, превышающим нормы — его использование небезопасно как для инвалидов, так и для родителей с детскими колясками. Величина допустимого уклона пандуса регламентируется СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» — актуализированная версия СНиП 35-01-2001, документ введен в действие 01.01.2013.

до 1:12 (8% или 4,76 градуса) — для временных сооружений и объектов инфраструктуры, при условии, что перепад высот между горизонтальными площадками менее 0,5 м и длина одного марша пандуса не более 6,0 м;
до 1:10 (10% или 5,71 градуса) — при перепаде высот полов менее 0,2 м.

Как рассчитать угол наклона пандуса?

Вычисляется уклон пандуса с помощью формулы: наклон пандуса = H / L, где: H — перепад высот, который необходимо оборудовать пандусом, а L — длина горизонтальной проекции наклонного участка пандуса (нажмите для увеличения).

Например, нам необходимо рассчитать пандус для входа в здание, высота крыльца составляет 0,4 м. В данном случае необходимо использовать соотношение 1:12, составляя простую пропорцию получаем L=12*0.4 м = 4,8 м. Вычисляем длину наклонной поверхности пандуса = корень квадратный из (4,82+ 0,42) = 4,8 м Пандус может быть устроен без горизонтальных площадок, так как длина его наклонных поверхностей менее 6 м.

Если говорить о единицах измерения, то наклон пандуса может быть выражен в градусах, процентах и в виде отношения высоты к длине:

Норматив Соотношение Значение в % Значение в градусах Единицы измерения уклона пандуса

стандартный по СП 59.13330. 2012	1:20	5%	2,86 градуса
для временных сооружений	1:12	8%	4,76 градуса
при перепаде высот до 0,2 м	1:10	10%	5,71 градуса

Уклон пандуса по СНиП 35-01-2001 и СП 59.13330.2012

В обозначенных выше документах есть разночтения по стандартной величине уклона пандусов, так в СНиП 35-01-2001 допустимый уклон пандуса составляет 1:12 (или 8%), в то время как по СП 59.13330.2012 — он равен 1:20 (или 5%).

Учитывая, что СНиП 35-01-2001 является национальным стандартом, утвержденным Распоряжением Правительства РФ от 21 июня 2010 г. № 1047-р, а также, если заказчиком не выдвигается требование спроектировать пандус по СП 59.13330.2012, предлагаем своим клиентам проектирование и изготовление пандусов по нормативам, обозначенным в СНиП 35-01-2001, т.е.:

допустимый уклон пандуса — 1:12 (или 8%, или 4,76 градуса).

Пандус для маломобильных групп

Калькулятор уклонов — посчитать онлайн

Чтобы посчитать уклон кровли, крыши, трубопровода, пандуса, лестницы, дороги, реки и т. п. воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Посчитать уклон

Посчитать превышение

Посчитать расстояние

Просто введите значения и выберите единицы измерения уклона.

Теория

Как посчитать уклон

Для того чтобы посчитать уклон вам, для начала, необходимо знать расстояние (L) и превышение (h). Далее следуйте формулам:

В процентах:

Уклон в % = h / L ⋅ 100

В промилле:

Уклон в ‰ = h / L ⋅ 1000

В градусах:

Уклон в ° = arctg(^h/_L)

Пример

Для примера рассчитаем уклон дороги в процентах: на дистанции в L = 500 м дорога поднимается на h = 30 м:

Уклон дороги = 30/500 ⋅ 100 = 6%

Как посчитать превышение

Чтобы вычислить превышение (h), надо знать расстояние (L) и уклон (в процентах, в промилле или в градусах).

Если уклон в процентах (%):

h =^{L ⋅ Уклон в %}/₁₀₀

Если уклон в промилле (‰):

h =^{L ⋅ Уклон в ‰}/₁₀₀₀

Если уклон в градусах (°):

h = L ⋅ tg(α) , где α — уклон в градусах

Пример

Для примера найдём превышение h, если расстояние L= 5м, а угол уклона α=45°:

h = 5 ⋅ tg(45) = 5 ⋅ 1 = 5 м

Как посчитать расстояние

Для того чтобы посчитать расстояние (L) необходимо знать превышение (h) и уклон (в процентах, в промилле или в градусах).

Если уклон в процентах (%):

L = ^h / _{Уклон в %} ⋅ 100

Если уклон в промилле (‰):

L = ^h / _{Уклон в ‰} ⋅ 1000

Если уклон в градусах (°):

L = h / tg(α), где α — уклон в градусах

Пример

Для примера посчитаем расстояние (L), которое потребуется железной дороге, чтобы подняться на (h =) 6 м при угле подъёма 30‰:

L = 6 / 30 ⋅1000 = 200 м

См. также

Угол уклона пандуса

Основным нормативным документом для определения уклона пандуса и его длины в РФ является СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» С Изменением №1 — актуализированная версия СНиП 35-01-2001.

Допустимые значения угла наклона пандуса

— Допустимый угол уклона пандуса должен быть не круче 1:20 (5%), а максимальная высота одного подъема (марша) пандуса не должна превышать 0,8 м.
— При перепаде высот пола на путях движения 0,2 м и менее допускается увеличивать уклон пандуса до 1:10 (10%)
— На временных сооружениях или объектах временной инфраструктуры допускается максимальный уклон пандуса 1:12 (8%) при условии, что подъем по вертикали между площадками не превышает 0,5 м, а длина пандуса между площадками — не более 6,0 м.

— Пандусы при перепаде высот более 3,0 м и расчетной длиной более 36 м следует заменять лифтами, подъемными платформами и т.п
— В соответствии с приказом Минстроя России №750/пр от 21 октября 2015 г. «Об утверждении изменений №1 к СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» «При проектировании реконструируемых, подлежащих капитальному ремонту и приспосабливаемых существующих зданий и сооружений уклон пандуса принимается в интервале от 1:20 (5%) до 1:12 (8%)».

Что обозначают цифры

1:10 — 10% — один к десяти, т.е. при перепаде высот в 1 м, длина пандуса должна быть 10 м, при высоте 0,5 м — длина пандуса должна быть 5 м и т.д.

В этом случае угол уклона пандуса будет соответствовать 5,7 градусам.

1:12 — 8% — один к двенадцати, т.е. при перепаде высоты в 1 м, длина пандуса должна быть 12 м, при высоте 0,5 м — длина пандуса должна быть не менее 6 метров и т.д.
Угол уклона пандуса будет равен 4,8 градусам.

1:20 — 5% — один к двадцати, т.е. при перепаде высот 1 м, длина пандуса должна быть 20 м, при высоте 0,5 м — 10 м.
Угол уклона пандуса будет равен 2,9 градусам.

Какой длины делать пандус?

Расчет длины пандуса в зависимости от высоты
Высота пандуса, м	Длина пандуса, м
Высота пандуса, м	1:10=10%=5,7° (используется при перепаде высот менее 0,2 м)	1:12=8%=4,8° (для временных, приспосабливаемых и реконструируемых сооружений)	1:20=5%=2,9° (стандартный показатель)
0,1	1	1,2	2
0,2	2	2,4	4
0,3	3	3,6	6
0,4	4	4,8	8
0,5	5	6	10
0,6	6	7,2	12
0,7	7	8,4	14
0,8	8	9,6	16
0,9	9	10,8	18
1	10	12	20
1,1	11	13,2	22
1,2	12	14,4	24
1,3	13	15,6	26
1,4	14	16,8	28
1,5	15	18	30

Зеленый — допустимые значения, красный — недопустимые.

Если Вам необходимо самостоятельно рассчитать угол уклона пандуса, зная его длину и высоту, то необходимо воспользоваться следующей формулой
arcsin(h/L), где h — высота, L — длина.
Для этого воспользуйтесь инженерным калькулятором

Примеры внедрений

Уклоны. Теория — на уровне глаз — ЖЖ

Как было сказано ранее, по одному из определений уклон это тангенс угла. С большим интересом узнал, что он равен коэффициенту сцепления. Вот тут и начинает прояснятся тайный смысл предупреждающих дорожных знаков 1.13 и 1.14 (крутой спуск / подъём).

Коэффициентом сцепления называется отношение двух сил – силы, необходимой для сдвига машины с заблокированными колесами, и силы тяжести, прижимающей машину к дороге. Так мы легко можем получить коэффициенты сцепления для сухого асфальта – 7000/10000 = 0,7, для грязной дороги – 3000/10000 = 0,3, и для льда – 1000/10000 = 0,1.
Например, автомобиль, стоящий на сухом асфальтированном уклоне с коэффициентом сцепления 0,7, начнет сползать вниз, если тангенс угла наклона при этом будет равен 70% (это уклон около 35 градусов, вряд ли вы когда-нибудь встретите такой).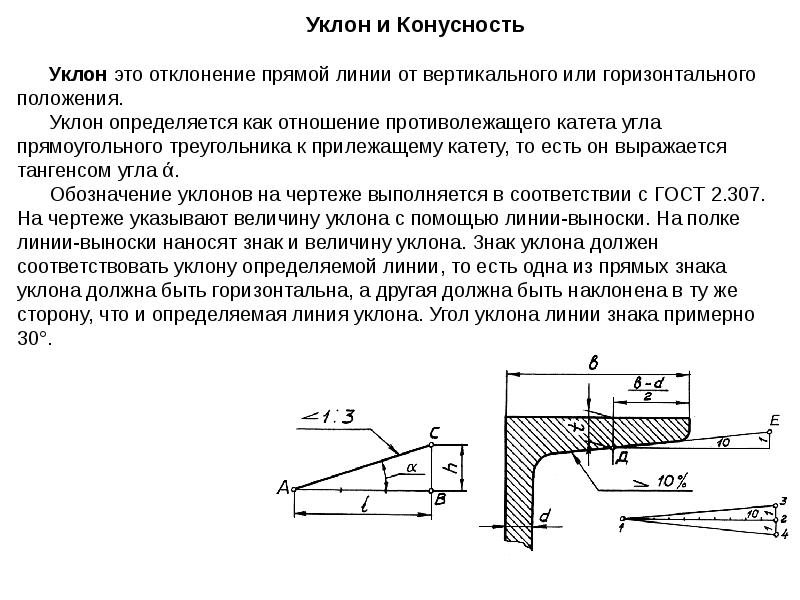 Но, кроме дорог, существуют улочки старых городов, особенно приморских, с углами наклона, существенно превышающими всевозможные нормативы. [2]

И в чём практическая ценность этой информации? Вот в чём: если на дворе гололёд, то на дороге с уклоном в 10% и более остановившаяся машина не удержится, будет скатываться.
К тому же, «при движении в сырую погоду вниз по асфальтированному уклону крутизной 20% эффективность торможения падает наполовину. И очень часто вам придется двигаться по мокрому льду с коэффициентом сцепления 0,1 и менее. А это значит, что вы должны внимательно отслеживать предупреждающие дорожные знаки 1.13 и 1.14. Их устанавливают, когда тангенс угла уклона приближается к 10%. Если вы пренебрежете этими знаками и остановитесь на подъеме, то в лучшем случае – не сможете сдвинуться с места. А уж если затормозите на спуске, машину может занести. Старайтесь тормозить двигателем на длительных спусках.» [2]
Вот о чём предупреждают знаки.

Кстати, есть знаки и меньше 10%, поэтому стало интересно в каких случаях их устанавливают.
ГОСТ Р 52289-2004 «Правила применения дорожных знаков, разметки, светофоров, дорожных ограждений и направляющих устройств», п. 5.2.16:
4% — если длина участка дороги на спуске или подъёме больше 600 метров при данном уклоне.
5% если больше 450 метров
6% если больше 350 метров
7% если больше 300 метров
8% (и более) если больше 270 метров.
Там же указаны и другие случаи, как например расстояние видимости, но сейчас они нас не интересуют.

Причины: почему проценты?

При рассмотрении темы уклонов всегда возникает вопрос, а почему уклон измеряют в процентах, а не в привычных градусах? По этому поводу слышал несколько версий:

а) Карты
Так проще вычислять уклон рельефа на карте или на строительном плане. Рельеф на картах обозначается линиями — горизонталями. Это замкнутая линия, которая получается если мысленно сделать сечение на какой-либо высоте и посмотреть сверху. Проще это представить если вспомнить линию уреза воды реки или водоёма, это тоже своего рода горизонталь.

Горизонтали, т.е. горизонтальные сечения, проводятся через определённое постоянное расстояние по высоте, о чём указывается в примечаниях. Зная высоту сечения горизонталей и определив на карте расстояние между ними можно получить уклон. Чем ближе друг к другу на карте изображены горизонтали, тем рельеф круче.

б) Погрешность
Построить угол, заданный в градусах, так сказать «в натуре» на строительной площадке, задача не из простых, а построить точно и вовсе запредельная. Небольшие величины уклона в градусах имеют вид десятичных дробей, а ведь погрешность даже в 1° на 10 метров длины даст ошибочные 17 сантиметров высоты. Так же, проценты величина относительная, и потому уклон, выраженный в процентах, можно построить имея в распоряжении только рулетку (или иной инструмент для измерения длинны) и уровень.

в) Неравномерность
Дорога, на протяжении всего спуска (подъёма), имеет неравномерный уклон. В каждый отдельный момент угол разный, и поэтому проще посчитать сколько составляет горизонтальная длинна участка спуска (подъёма), и на сколько изменилась высота относительно начала спуска (подъёма).

seyfulmulyukov.livejournal.com / 1avtorul.ru

Все эти версии вполне имеют право на жизнь. Общим для них является то, что для нахождения величины уклона используются меры длинны, которые всегда есть под рукой, а это практично. Что касается дорожных знаков, то более правдоподобной выглядит третья версия (неравномерность уклона), а для строительства дорог вторая (погрешность построений).
Есть ещё Международная Конвенция о дорожных знаках и сигналах за 1968 год, и Европейское соглашение 1971 года, дополняющее эту Конвенцию, по которой на предупреждающих знаках крутизна уклонов и подъемов указывается в процентах. [3]

Что стоит за цифрами, например 1/12 или 10%, много это или мало, как это выглядит и где применяется, рассмотрим в следующий раз на примерах из жизни.

Использованные материалы

1. Словари и энциклопедии на Академике © Академик
2. Материалы сайта «Школа жизни» © Shkolazhizni.ru
3.

Википедия © Wikipedia
—

Расчет параметров скатной кровли на примере вальмовой

Чтобы рассчитать кровельные материалы, необходим документ, который по ГОСТ 21.501-93 «Правила выполнения архитектурно-строительных чертежей» называется план кровли (крыши). Для корректного расчёта параметров достаточно вида крыши сверху с обозначенными направлениями скатов, длин проекций и высотными отметками.

На рисунке представлен общий вид дома с конструкцией вальмовой крыши. Данный тип крыши состоит из 4-х скатов (плоскостей): два треугольных ската (вальмы) и две трапеции.

Для точного определения размеров кровли необходимо знать уклоны скатов кровли (крыши). Уклон ската – угол наклона ската по отношению к горизонту. Может выражаться в градусах, в процентах, дробях.

Если на плане кровли не указаны уклоны, измерить их можно с помощью транспортира по планам фасадов. С большей степенью точности можно вычислить, зная проекционные и высотные размеры кровли. Так как отношение этих двух величин постоянное для конкретного уклона, градусность будет определена предельно точно.

Интересные факты, известные из курса школьной геометрии:

Если проекция ската равна изменению его высоты, уклон кровли будет равным 45 градусов;
Длина ската, уклон которого равен 30-ти градусам в два раза больше его высоты. А длина ската с уклоном 60 градусов в два раза больше её проекции.

Для первого примера отношение высоты к проекции 1:1, а длина ската будет больше её проекции в 1,414 раза. Таким образом, 1,414 — коэффициент уклона ската с уклоном 45 градусов. Для уклона 60 градусов этот коэффициент равен 2,000, а для 30 – 1,155.

Следовательно, параметры ската в рамках конкретной кровли взаимосвязаны, и могут быть вычислены при известности двух из них.

Следующая задача, которую предстоит решать специалисту в ходе расчёта кровельных материалов, заключается в определении площади кровли, а так же суммарных длин всех её одноименных элементов: коньков, хребтов, карнизов. Для других конфигурация кровли могут быть ещё: ендовы, примыкания, фронтоны (щипцы, торцы) и так далее.

При определении площади следует разбить её на составляющие прямоугольники, треугольники, трапеции, при необходимости, круги и другие фигуры.

Относительно рассматриваемой крыши, план кровли разделён естественным образом на два треугольника и две трапеции.

На следующем рисунке планы кровли и двух основных фасада:

Приступим к расчету геометрических параметров крыши:

L_{карниза} = (10 + 6 )*2 = 32 м
L _конька = 4 м

Определим длины скатов. Они равны между собой исходя из плана кровли.

Смотрим на план кровли и видим, что длина ската по плану кровли составляет 3м. Однако это все же не искомая длина ската, а всего лишь проекция этой длины на горизонтальную плоскость.

Чтобы преобразовать проекцию длины в действительный размер достаточно умножить проекцию на коэффициент 1,155 (для 30 градусов):

L_ската= 3м * 1,155 = 3,465 м.

Также, длину ската можно найти по теореме Пифагора, если известна высота крыши (H = 1,732 м):

(L _ската) ² = H ² + (проекция длины ската) ² = (1,732) ² + (3) ² = 2,999824 + 9 =11,999824
L _ската=3,465 м.

Найденная длина ската(скатов) является определяющей высотой фигур (трапеции и треугольника) при расчете площадей:

S_кровли = S_{ската 1} + S_{ската 2} + S_{ската 3} + S_{ската 4}
S _{ската 1} = S_{ската 3} и S _{ската 2} = S_{ската 4}

По формуле площади треугольника:
S _{ската 1}= (6*3,465)/2 = 10,395 м²

По формуле площади трапеции:
S_{ската 2} = ((10+4)/2)*3,465 = 24,255 м²

Итого общая площадь кровли:
S_кровли = 10,395 + 10,395 + 24,255 + 24,255 = 67,3 м²

Есть самый быстрый способ определения нашей искомой площади, заключается он в умножении площади проекции крыши (габариты крыши по плану кровли, 6м х 10м) на коэффициент 1,155 (по аналогии с определением длины ската):

S _кровли = 6*10*1,155 = 69,3 м²

Оставшийся параметр – длину ребра(хребта) можно также определить по теореме Пифагора:

( L _{ребра(хребта)} ) ² = 3 2 + (длины ската) ² = ( 3 ) ² + (3,465) ² = 9 + 12,006225 = 21,006225
L_{ребра(хребта)} = 4,583 м

Существует также коэффициент пересчета для определения искомых длин ребер, для этого достаточно умножить длину ребра(хребта) по плану кровли на коэффициент пересчета (30град./30град.), равным значению 1,08.

Итак:

(L _{проекции хребра(хребта)}) ² = 3 2 +3 2 = 18
L_{проекции хребра(хребта)} = 4,24264068711
L_{ребра(хребта)}= 4,24264068711 *1,08 = 4,583 м

Сумма длин всех ребер(хребтов): L _{ребер(хребтов)} = 4,583*4 = 18,332 м

После того как все геометрические параметры крыши определены, мы сможем подобрать и рассчитать любой кровельный материал по нашему выбору.

Вариант расчета кровли BRAAS, модель «Франкфуртская»:

(Минимальный рекомендуемый угол крыши для данной модели составляет 16 градусов, удовлетворяет нашим требованиям).

Внешние габариты одной черепицы «Франкфуртская» составляют 330х420мм.

Поскольку черепица укладывается с нахлестом и с учетом стыковки черепицы между собой через замковое соединение полезная площадь покрытия одной черепицы будет несколько меньше и составит 300х330мм.

Полезная площадь покрытия для всех видов черепиц всегда разная и обусловена широким разнообразием профилей и их размеров.

При размерах 300х330мм расход на 1м² составляет:

1м²/(0,3м * 0,33м) = 10,1шт./м²

Общее количество рядовой черепицы на покрытие всей крыши:

10,1*69,3 м² = 700 шт.

Принимая во внимание возможный бой черепицы при доставке/разгрузке/монтаже, а также некоторые отклонения в фактических размерах от данных в проекте, обязательно учитывается технологический запас материала. Величина запаса зависит от геометрической сложности кровли и должна приниматься индивидуально для каждого крыши. Для вальмовой крыши будет достаточно 5%. Запас очень важен при расчете кровельного покрытия, т.к. предостерегает нас от нехватки материала при монтаже кровли.

В итоге, с учетом запаса нам необходимо:

700 шт. + 5% = 735шт.

Количество начальной хребтовой черепицы:

4 шт.

Количество рядовой коньковой черепицы (расход 2,5шт./мп):

2,5*18,332 = 46 шт.
46 шт. — 4 шт. (начальные хребтовые) = 42 шт.

Вальмовая черепица: 2 шт. (устанавливается на место пересечения конька и двух ребер)

А теперь, предлагаем посмотреть как выглядит подробный расчет кровельного покрытия в нашей компании с учетом крепежа и всех необходимых аксессуаров:

А также раздел 2 с крепежом и необходимыми аксессуарами:

В данной статье мы разобрали с вами расчет скатной типовой крыши имея при себе лист бумаги, карандаш и немножко знаний из школьной программы геометрии. Сложные кровли с большим количеством скатов разных геометрических форм, сложных многоугольников, а также криволинейных поверхностей (конусов, сфер и т.д.) рассчитываются программно на ПК в специальных инженерных пакетах. Это в значительной мере облегчает процесс расчета, экономит время и предостерегает нас от возможных арифметических ошибок при расчете.

Расчёт угла наклона крыши | Альфалес

Поскольку от его величины зависит и количество кровельного материала, то выбор угла наклона и его предварительные расчеты производят до начала закупки выбранного кровельного материала.

Что на него влияет

В зависимости от величины уклона скатов крыши зависит особенность ее эксплуатации.

Принято выделять 4 типа крыш: высокие — с углом в 45–60 градусов; скатные — с наклоном от 30 до 45 градусов; пологие — с углом уклона 10–30 градусов; плоские — с углом 10 градусов и меньше.

На выбор величины этого параметра оказывают влияние, в первую очередь, природные факторы, которые характерны для данной местности.

Ветровая нагрузка

Сильный ветер самое большое давление оказывает на кровли высокие. Потому что такие кровли из-за большого угла наклона имеют очень большую площадь. У большой площади поверхности очень высока парусность. Соответственно, очень велика нагрузка на всю конструкцию стропильной системы. И если вы решили устраивать именно высокую кровлю с очень большим уклоном, то следует позаботиться и об очень прочном основании. Однако в районах, где преобладают сильные ветра, небезопасно устраивать и крыши плоские. При таком типе кровли на нижнюю часть ската будет оказываться повышенное давление при сильном ветре. И если крепление кровли будет ослабленным, может произойти срыв всей конструкции. Поэтому в районах, где сильные ветра бывают часто, рекомендуется устраивать скатные кровли с величиной наклона 25–30 градусов. Если же сила ветра невелика, то величина уклона крыши может равняться 30–45 градусов.

Нагрузка снеговая

Если в той местности, где строится дом, в холодное время года снегопад обильный, то следует строить кровлю с большим углом уклона. В этом случае высокая крыша вне конкуренции. На кровлях с большим уклоном снег не задерживается. Именно по этой причине во всех северных странах кровли на зданиях очень высокие (Швеция, Финляндия, Норвегия и пр.). Чем меньше угол уклона кровли, тем дольше выпавший снег будет находиться на скатах. Тем больший вес будет воздействовать на всю конструкцию. Если конструкция стропильной системы сделана с большим запасом прочности, то некоторый слой снега на крыше — это неплохо. Он обеспечивает небольшую дополнительную теплоизоляцию. Однако, если конструкция стропильной системы сооружения на большую нагрузку не рассчитана, то могут быть большие проблемы.

Выбираем уклон в зависимости от используемого кровельного материала

Прошли те времена, когда для покрытия использовали всего два вида кровельных материалов: черепицу и шифер. Каждый материал имеет свои индивидуальные технические характеристики и это при расчете необходимого значения угла наклона обязательно следует учитывать. Ведь может произойти так, что понравившийся вам материал по своим параметрам просто не подойдет.

Минимальный угол наклона

Существует понятие минимального значения этого параметра. Для каждого из материалов этот параметр свой. И если угол наклона, полученный в результате ваших расчетов, окажется меньше, чем минимальная величина для выбранного вами кровельного материала, то использовать его для устройства кровли нельзя.

В дальнейшем может возникнуть очень много проблем, если нарушить это правило:

для любых штучных наборных кровельных материалов, таких как черепица или шифер, минимальная величина уклона составляет 22 градуса. Именно при таком значении на стыках не скапливается влага и внутрь крыши влага не просачивается;
угол наклона для рулонных материалов (рубероид, бикрост и пр.) зависит от того, какое вы планируете укладывать количество слоев. Если три слоя, то уклон может составлять 2–5 градусов. Если же два слоя, то его требуется увеличить до 15 градусов;
производители профнастила рекомендуют при устройстве кровли из этого материала устраивать угол уклона 12 градусов. Профнастил можно использовать и при меньших значениях, но в таком случае необходимо выполнить проклейку стыков листов герметиком;
для металлической черепицы значение этого параметра равняется 14;
для ондулина — это величина в 6 градусов;
минимальный уклон для мягкой черепицы равняется 11 градусам. Но при этом обязательное условие — сплошная обрешетка;
для мембранных кровельных покрытий не существует жестких требований по минимальному значению этого параметра.

Это о минимальных величинах. Дадим совет — придерживайтесь этих правил, чтобы посреди зимы не пришлось всю кровлю перестилать.

Если в регионе дожди и снега случаются часто, то оптимальной будет крыша, угол наклона скатов у которой будет составлять 45 — 60 градусов. Ведь с кровли необходимо как можно скорее снимать нагрузку от воды и снега. Потому что прочность стропильной системы не беспредельна. А благодаря большому уклону кровли дождь и снег будут сходить максимально быстро.

Если в регионе, где построен дом, постоянно сильные ветра, то с крышей поступают иначе. При меньшем наклоне снижается ее парусность. И не возникает запредельных нагрузок на кровельный материал и стропила. Также не произойдет срывания крыши при резких порывах ветра. При этом оптимальный угол уклона кровли равняется 9–20 градусов.

Очень часто в регионе есть и снега, и ветер. Например, Оренбургская область. В таком случае выбирают среднее значение угла наклона. Как правило, его величина находится в диапазоне 20 — 45 градусов. Если вы обратите внимание, большинство скатных крыш имеют именно такое его значение.

Рассчитываем его величину

Для односкатной

Поскольку односкатная крыша опирается на стены, имеющие разную высоту, то формирование заданного угла наклона производят, просто поднимая одну из стен. Проводим вдоль стены перпендикуляр L сд, берущий свое начало в точке, где оканчивается короткая стена и опирающийся на стену, имеющую максимальную дину. В итоге образуется прямоугольный треугольник.

Для того, чтобы рассчитать длину стороны L bc, надо воспользоваться тригонометрической формулой.

Если длина стены L сд равняется 10 метрам, то, чтобы получить угол наклона 45 градусов, длина стены L bc должна ровняться 14.08 метра.

Для двускатной

Принцип расчета для двускатной крыши похож на предыдущий принцип.

Рассмотрим пример. Катет С — это половина ширины здания. Катет, а — это высота от перекрытия до конька. Гипотенуза является длиной ската. Если нам известны любые два параметра, то величину угла наклона можно легко рассчитать с использованием калькулятора.

Если ширина равна 8, а высота — 10 метров, то следует пользоваться формулой:
cos A = c+b

Ширина с = 8/2 = 4 метра.

В итоге формула выглядит так:

cos A = 4/10 = 0.4

По таблицам Брадиса находим значение угла, которому соответствует данная величина косинуса. Он равняется 66 градусов.

Для четырехскатной

И снова не обойтись без рулетки и таблиц Брадиса. Зная несколько параметров, можно без проблем вычислить другие. В том числе и угол наклона четырехскатной крыши. Следует помнить о том, что все размеры необходимо снимать максимально точно. А измерить уклон уже построенной крыши поможет специальный инструмент — уклономер. Ведь если вы ошибетесь, то углы наклона, длины и площади могут быть не верны. А значит, вы ошибетесь в количестве требуемого материала или прочность кровли окажется ниже запланированной.

как посчитать, методы, как перевести градусы в промилле

Существуют нормативы на уклоны при проектировании различных коммуникаций и сооружений, которыми руководствуются в своей работе архитекторы и строители. Пользоваться можно любыми размерностями, в том числе и градусами. На практике принято крутые склоны обозначать в градусах, а пологие — в процентах и промилле.

Способы вычисления склона в процентах

Единицей измерения крена, в зависимости от его величины, бывают градус, процент, промилле — тысячная доля целого числа: 1‰ = 1/10% = 1/1000 от 1. Физический смысл уклона — отношение перепада высот к длине участка, на котором это наблюдается. По сути — тангенс угла: превышение 12 метров на отрезке дороги в сто метров выражается величиной 0,12 (тангенс) = 12% = 120 ‰. То есть чтобы сделать расчёт уклона в промилле, надо умножить процентный показатель на десять.

При выполнении планировочных работ на земельном участке приходится прибегать к измерениям крутизны косогоров. Сделать это можно несколькими методами:

С помощью нивелира выполняются все необходимые измерения, а потом несложными вычислениями формируется уклон в процентах. Как считать: перепад высот делится на расстояние между точками замеров, и результат умножается на сто процентов.
По плану земельного участка, если на нём вынесены отметки рельефа местности. Разница высот между необходимыми точками считывается с рисунка, а расстояние замеряется масштабной линейкой. Дальнейшие вычисления аналогичны предыдущему способу.

Кровельщики часто сталкиваются с необходимостью определить фактический скат крыши, и знают, как рассчитать уклон с помощью специального инструмента, называемого уклономер. Конструкция приспособления несложная: на рейке закреплена рамка с закреплённым внутри транспортиром и маятником, имеющим груз и указатель. Основу прибора ставят на нижнюю поверхность измеряемого участка кровли, и стрелка обозначит угол.

Определение угла наклона через тангенс

Из тригонометрии известно, что тангенс — дробь, в основании которой прилежащий к углу катет, а поверх — противолежащий (перепад высот). Чтобы определить уклон кровли в процентах и градусах через тангенс, понадобится выполнить замеры:

высоты от потолочного перекрытия до конька кровли;
расстояния от края ската до проекции верхней линии смыкания двух плоскостей.

Сделав несложные расчёты, получают некоторое значение и по таблице Брадиса или с помощью инженерного калькулятора находят соответствующее число градусов для искомого угла. Как посчитать уклон в процентах — определено выше: высоту конька делят на половину ширины чердачного перекрытия, если скаты равной величины. Или на проекцию каждой из поверхностей кровли, когда размеры сторон различаются. Можно заметить, что это и есть тангенс уже определённого в градусах угла. Чтобы перейти к процентному выражению уклона, надо выполнить действие: значение tg *100, и результат получится в процентах.

Соотношение величин с уклоном крыши

Для каждого кровельного материала установлены допуски по наименьшему уклону. Другие факторы, влияющие на выбор угла скатов крыши:

способность комплексно защищать строение от внешних воздействий — техногенных и природных;
стойкость к ветровой нагрузке — крутые поверхности увеличивают парусность сооружения, это делает конструкцию уязвимой;
преобладание определённых решений архитекторов в отдельных регионах;
количество атмосферных осадков и загрязнений — на кровле с большим уклоном груз накапливаться не будет.

Строительные нормы и правила — СНиП II -26−76 регламентируют пологость скатов в процентах. Соотношение процентов и градусов для некоторых углов приведено в таблице.

Градус º	Тангенс	Процент, %	Промилле, ‰	Градус º	Тангенс	Процент, %	Промилле, ‰
1	0,0175	1,75	17,5	22	0,4040	40,40	—
5	0,0875	8,75	87,5	24	0,4452	44,52	—
10	0,1740	17,40	174	26	0,4878	48,78	—
12	0,2125	21,25	—	28	0,5318	53,18	—
14	0,2494	24,94	—	30	0,5773	57,73	—
16	0,2868	28,68	—	35	0,7001	70,01	—
18	0,3250	32,50	—	40	0,8390	83,90	—
20	0,3828	38,28	—	45	1,0000	100,0	—

Математические способы расчёта уклона применяются, когда особая точность не нужна, и измерения делают приблизительные. При необходимости вычислить точные показатели, пользуются современными измерительными приборами.

Пример вычисления: расстояние от края ската кровли до проекции линии сопряжения сторон — длина заложения, 5,2 м. Высота от чердачного перекрытия до верхней отметки кровли 2 метра. Уклон (тангенс угла) определяется действием: 2/5,2 = 0,3846. Ближайшее значение из таблицы — 20 градусов, что соответствует примерно 38%.

Другой вариант — с помощью угломера определили угол наклона кровли, его значение 5º. По соответствующей строке уклон поверхности составит 8,75 процента или 87,5 промилле.

Расчет уклона и общего уклона в архитектуре

Архитекторы постоянно предоставляют информацию об уклоне на своих чертежах, используя градиенты, градусы или проценты в зависимости от приложения. Например, крыши обозначаются градиентами, а поперечные уклоны тротуаров обычно обозначаются в градусах. Полезно понять, как рассчитать каждый метод.

Существует три различных способа указать наклон поверхности относительно горизонтальной плоскости: градусы, уклон и процент.

Расчет градиента уклона

Градиенты уклона записываются как Y: X, где Y — это единичная величина подъема, а X — это пробег. Оба числа должны использовать одни и те же единицы измерения. Например, если вы путешествуете на 3 дюйма по вертикали и 3 фута (36 дюймов) по горизонтали, уклон будет 3:36 или 1:12. Это читается как «наклон один из двенадцати».

Расчет процента уклона

Процент уклона рассчитывается так же, как и уклон.Преобразуйте приближение и бег в те же единицы, а затем разделите приближение на разбег. Умножьте это число на 100, и вы получите наклон в процентах. Например, подъем 3 дюйма, разделенный на 36 дюймов = 0,083 x 100 = уклон 8,3%.

Расчет уклона в градусах

Самый сложный способ вычисления наклона — в градусах, и для этого требуется немного математики средней школы. Тангенс данного угла (в градусах) равен подъему, деленному на пробег. Следовательно, величина, обратная тангенсу подъема, деленная на длину пробега, даст угол.

Таблица общих наклонов в архитектуре

В таблице ниже показаны некоторые распространенные уклоны. Полы с уклоном 1:20 не требуют поручней, но все, что круче 1:20, считается пандусом и требует поручней. Пандусы с уклоном 1:12 — это максимальный уклон, разрешенный правилами ADA, и для них требуются поручни. Федеральные коды ADA указывают, что максимальный поперечный уклон доступного маршрута составляет 1:48, что чуть больше 2%. Однако мы видели некоторые юрисдикции, которые разрешают максимальный поперечный уклон 1:50.

Градусов	Градиент	Процент
0,6 °	1: 95,49	1,0%
1 °	1: 57.29	1,7%
1,15 °	1 : 50	2%
1,19 °	1: 48	2,08%
2,86 °	1: 20	5%
4,76 °	1: 12	8 .3%
7,13 °	1: 8	12,5%
10 °	1: 5,67	17,6%
14,04 °	1: 4	25%
15 °	1: 3,73	26,8%
26,57 °	1: 2	50%
30 °	1: 1,73	57,7%
45 °	1: 1	100%
56.31 °	1: 0,67	150%
60 °	1: 0,6	173,2%
63,43 °	1: 0,5	200%
78,69 °	1 : 0,2	500%
89,43 °	1: 0,1	1000%
90 °	1: 0	инф.

Скаты крыши

Наклоны крыши идентифицируются с помощью описанного выше градиентного метода, где подъем меняется, но обычно длина спуска составляет 12.На некоторых очень крутых крышах вы можете увидеть инвертированный градиент, так что длина пролета меняется, но подъем сохраняется как 12.

Кровля с малым уклоном

Кровли с низким уклоном имеют уклон 3:12 или меньше. У них должна быть мембранная кровельная система для обеспечения водонепроницаемости.

Градиент крыши	Градусов	Процент
1/4: 12	1,19 °	2,08%
1/2: 12	2,39 °	4.17%
1: 12	4,76 °	8,3%
2: 12	9,46 °	16,67%
3: 12	14,04 °	25%

Крутые крыши

Все, что выше 3:12, считается крутой крышей и может быть покрыто металлическими панелями, черепицей или черепицей — эти крыши проливают воду и не считаются водонепроницаемыми.

Градиент крыши	Градусов	Процент
4: 12	18.43 °	33,33%
5: 12	22,62 °	41,67%
6: 12	26,57 °	50%
7: 12	30,26 °	58,33 %
8: 12	33,69 °	66,67%
9: 12	36,87 °	75%
10: 12	39,81 °	83,33%
11: 12	42.51 °	91,67%
12: 12	45 °	100%

Наклон Vs. Участок

Во время написания нашего последнего поста ко мне вернулся интересный вопрос. Это был тот же вопрос, который возник у меня, когда я получил датчик для крыши Holts после покупки его на eBay и начал внимательно его рассматривать. В чем разница между наклоном и шагом? Шаг 1/4 — уклон 6:12? Шаг 7/12 — наклон 14:12? Что, черт возьми, здесь происходит? Я занимаюсь кровлей 35 лет, и наклон и уклон всегда значили для меня одно и то же.

Ну, это отправило меня в Интернет. Мне нравится думать, что я хороший гуглер, поэтому я очень серьезно подумал, какие поисковые запросы лучше всего использовать, и придумал, «в чем разница между уклоном крыши и наклоном крыши». Я сказал вам, что я хороший гуглер. Я нажимаю Enter, и вуаля, на мой вопрос был дан ответ.

Здравствуйте, господин НАЧИ (это Национальная ассоциация сертифицированных домашних инспекторов для тех, кто не дружит). На сайте NACHI есть очень хороший ответ на мой вопрос.Конечно, статья NACHI больше ориентирована на черепицу, а Mule-Hide больше не делает ее, но информация об уклоне и уклоне не менее актуальна и для кровли с низким уклоном.

Вот что они сказали:

Наклон

Уклон — это наклон крыши, выраженный как отношение вертикального подъема горизонтального пролета, где пролег представляет собой некоторую часть пролета. Это соотношение всегда выражается в дюймах на фут.

Коэффициент наклона

Говорят, что крыша, которая поднимается на 4 дюйма на каждые 1 фут или 12 дюймов пробега, имеет уклон «4 на 12».Если подъем составляет 6 дюймов на каждые 12 дюймов пробега, то уклон крыши составляет «6 к 12».

Наклон можно численно выразить как отношение. Коэффициент уклона представляет собой определенное количество вертикального подъема на каждые 12 дюймов горизонтального пробега. Например, наклон «4 из 12» можно выразить как соотношение 4:12. Наклон «6 из 12» выражается как 6:12.

Наклон выражен:

как отношение; и
дюймов на фут

Шаг

Уклон — это наклон крыши, выраженный в виде дроби, полученной путем деления высоты на пролет, где пролет крыши — это расстояние между внешней стороной верхней плиты одной стены и другой.

Доля пека

Исторически слово «шаг» означало отношение высоты конька к полному пролету / ширине здания или отношение длины стропил к ширине здания. А тогда гребень обычно находился в середине пролета. В современной строительной практике этого больше нет. Гребень может быть размещен в любом месте пролета, непосредственно от середины до любой конечной точки пролета.

Говорят, что крыша, которая поднимается на 8 футов на 24-футовый пролет, имеет уклон «от 1 до 3».Если высота подъема составляет 4 фута при пролете 24 фута, то уклон крыши считается равным «от 1 до 6».

Шаг можно численно выразить дробью. Доля тангажа представляет собой определенную величину вертикального подъема по всему пролету. Например, для крыши с подъемом 4 фута и пролетом в 24 фута шаг составляет от 1 до 6, что может быть выражено как дробь 1/6. Шаг от 12 до 24 дюймов выражается как 1/2.

Итак, что я узнал? Не думаю, что могу сказать это лучше, чем статья NACHI:

«Термины« шаг »и« наклон »часто используются как синонимы, что неверно.Они не означают одно и то же. А наклон дает более ценную информацию, чем шаг, как определено в этой статье ».

Еще раз спасибо NACHI.org и вот ссылка на всю статью: https://www.nachi.org/roof-slope-pitch.htm

Вернуться в блог Калькулятор рампы
. Стандарты рамп ADA и другое
Если вам сложно поднять коляску или инвалидную коляску на несколько ступенек, мы подготовили для вас отличный инструмент — калькулятор аппарели .Вы можете не только проверить соответствующий уклон пандуса , но мы также дадим вам подсказки о конструкции пандуса в целом. Не нужно беспокоиться о таких вещах, как размер рампы, посадочный размер или поручни! Если вы хотите узнать, как построить пандус, соответствующий требованиям ADA к пандусу , мы включили в него советы. Кроме того, мы рекомендуем прочитать подробный параграф уклона пандуса ADA ниже. Готовы? 🔨
Как рассчитать уклон пандуса?
Прежде чем мы покажем вам, как рассчитать уклон пандуса, нам сначала нужно объяснить условные обозначения единиц уклона.Наклон можно выразить разными способами, но давайте сосредоточимся на трех самых популярных формах:
Передаточное отношение подъема к ходу
Это отношение одной части подъема к соответствующей части пробега. Его можно выразить в нескольких различных обозначениях: 1: 8, 1/8, 1 из 8, например. Например, при соотношении 1:12 для каждой единицы вертикального подъема необходимо иметь 12 единиц горизонтального хода, поэтому 1 дюйм подъема означает, что необходимо 12 дюймов (1 фут) горизонтального пространства. Обычные уклоны 1:12, 1:20, 1: 8.
наклон [коэффициент] = подъем: ход
Уголок
Это угол между аппарелью и спуском (или, другими словами, угол наклона к горизонтали). Этот угол обычно выражается в градусах, хотя возможны и другие угловые единицы. Чтобы вычислить угол наклона, используйте арктангенс:
наклон [угол] = arctan (подъем / спуск)
В процентах
Указание уклона (уклона) в процентах является наиболее распространенным способом описания уклонов в США и Европе.Будьте осторожны — 100% уклон эквивалентен не 90 градусам, а 45 градусам. Рассчитывается по тангенсу угла наклона:
наклон [%] = 100% * подъем / ход = 100% * тангенс угла наклона
Наклон в долях, процентах и градусах
После этого вступления о модулях уклона, давайте вернемся к сути вопроса: как рассчитать уклон рампы?

Ну, это зависит от того, какая информация у вас есть — если вы знаете рост и бег (самый простой случай), вы можете использовать формулы, упомянутые выше.Однако вы можете знать подъем и гипотенузу прямоугольного треугольника, который образует наклон. В этом случае вы можете рассчитать пробег прямо по формуле Пифагора:
ход ² + подъем ² = гипотенуза ²
пробег = √ (гипотенуза ² - подъем ²)
В данном калькуляторе уклона пандуса для инвалидных колясок длина пандуса является гипотенузой, но для лестниц — длиной стрингера, а для кровли — длиной стропила.
В качестве альтернативы вы можете найти наклон с помощью обратных функций:
обратный грех, если вы знаете подъем и гипотенузу:
наклон [%] = arcsin (подъем / гипотенуза)
обратный косинус, если вы знаете пробег и гипотенузу:
наклон [%] = arccos (подъем / гипотенуза)
Склоны пандуса ADA
Стандарты ADA 2010 г. (Закон об американцах с ограниченными возможностями) устанавливают некоторые минимальные требования к новым общественным учреждениям.Помимо множества различных стандартов доступности, он содержит рекомендации по строительству пандусов. В этом абзаце мы более подробно рассмотрим склоны рампы ADA.
Согласно стандартам ADA, для любого пандуса должен использоваться наименее крутой уклон. Помимо этой информации, что именно говорится в руководстве?
1:12 — максимальный уклон пандуса для новостроек
1:16 — удобный уклон
1:20 — это минимальный уклон — ниже этого значения он не считается пандусом (например, e.г., поручни не нужны)
В каждом случае максимально допустимый подъем составляет 30 дюймов (760 мм). Эти три значения наклона кривой ADA предварительно установлены в нашем калькуляторе рампы.
Если существующих площадок, зданий и сооружений имеют ограниченное пространство, могут быть разрешены более крутые склоны пандусов ADA. Однако действуют более строгие ограничения на максимальный рост:
Наклон Максимальный подъем
дюймов миллиметров
от 1: 8 до <1:10 3 дюйма 75 мм
1:10 до <1:12 6 дюймов 150 мм
Помните, что ADA запрещает уклоны круче 1: 8.
Прочие требования к рампе ADA
При строительстве пандуса, будь то для вашего дома, общественного пространства или временного использования, вам нужно подумать о нескольких вещах, кроме наклона и подъема пандуса:
1. Ширина в свету
Минимальная ширина пандуса в свету составляет 36 дюймов (91,5 см). Не забудьте учесть крепление поручней при проектировании пандуса.
2. Посадки
Каждый пандус должен иметь ровные площадки вверху и внизу каждой секции, особенно если у пандуса несколько секций (поворотов).Следующие особенности посадки являются существенными:
Минимальная длина площадки составляет 60 дюймов (1525 мм), а ширина площадки должна быть не менее ширины пролета аппарели .

Вам необходимо обеспечить достаточно места для маневров: если конструкция аппарели меняет направление (поворот на 90 градусов), то минимальный посадочный размер составляет 60 «x60» :
Не забудьте добавить еще больше места для пандусов обратного хода.
3. Поручни
Каждый раз, когда на рампе:
подъем более 6 дюймов (15 см) или
пробег более 72 дюймов (183 см),
, то поручни необходимы с обеих сторон, чтобы соответствовать стандартам ADA. Вы найдете более подробную информацию в параграфе 4.8.5 документа ADA Ramp
.
4. Другими важными факторами являются:
поперечный уклон (развал) аппарелей не может превышать 1:50,
рампа должна быть сделана из соответствующего материала для предотвращения скольжения и скольжения ,
защита кромок и удлинители поручней,
с учетом погодных условий, если это пандус уличный ( правильный дренаж ).
Калькулятор уклона пандуса для инвалидных колясок. Расчет🖩, проектирование📝 и DIY🔨
Если вам интересно, как построить пандус, наш калькулятор пандуса будет большим подспорьем в его проектировании и строительстве. Используйте его либо в качестве калькулятора наклона пандуса ADA, чтобы соответствовать государственным стандартам, либо в качестве инструмента для расчета пандуса, специально адаптированного к вашим потребностям.
Теперь, как использовать этот калькулятор уклона пандуса для инвалидных колясок?
Выберите приложение аппарели .Предположим, мы хотим соответствовать требованиям ADA к рампе, и хотим сделать удобный аппарель. Выберите вариант 1:16 из раскрывающегося списка.
Выберите тип рампы . Вы можете выбрать прямой пандус, пандус с одним поворотом или пандус с обратным поворотом. Выберите последнее для нашего примера.
Введите вертикальный подъем . В нашем случае нам нужно преодолеть пять 7-дюймовых ступеней. Введите 35 в поле подъема (или просто 5 * 7).
Вот и все — наш калькулятор уклона пандуса ADA покажет вам ваши результаты :
наклон : 3,58 ° (6,25%)
пробег : 46,67 футов
длина пандуса : 46,67 фута
полезная информация для строительства двух съездов :
Для двух пандусов одинаковой длины каждая должна иметь длину 23,38 фута. Конечно, вы можете разделить его по-разному, в зависимости от доступного места.Только помните, что для такого уклона максимальное расстояние между посадочными площадками составляет 40 футов.
Дополнительно вы получите несколько советов по посадочному размеру и ширине аппарели.
Это было не так уж сложно, правда?
Более того, наш инструмент еще более универсален, так как вам не нужно выбирать из предустановленных приложений . Например, если вам нужен пандус с определенным углом, просто введите это значение в соответствующее поле (например, 5 °), заполните поле подъема, и длина разбега и пандуса будет рассчитана для вас.Кроме того, вы можете нажать кнопку расширенного режима , чтобы отобразить уклон в форме соотношения, а затем вы можете ввести значение соотношения уклона (например, если вам нужно соотношение 1: 8 для старых зданий).
Надеемся, что наш калькулятор рамп будет вам полезен. Оцените этот калькулятор и расскажите, что вы думаете о нем и можно ли его как-либо улучшить.
Калькулятор уклона
По определению, наклон или уклон линии описывает ее крутизну, уклон или уклон.
Где
м — уклон
θ — угол наклона
Если известны 2 точки

Если известны 1 точка и наклон
Уклон, иногда называемый в математике градиентом, — это число, которое измеряет крутизну и направление линии или участка линии, соединяющей две точки, и обычно обозначается м . Обычно крутизна линии измеряется абсолютным значением ее наклона, м .Чем больше значение, тем круче линия. Учитывая м , можно определить направление линии, которую описывает м , на основе ее знака и значения:
Линия увеличивается и идет вверх слева направо, когда m> 0
Линия убывает и идет вниз слева направо, когда m <0
Линия имеет постоянный наклон и является горизонтальной при m = 0
Вертикальная линия имеет неопределенный наклон, так как это приведет к дроби с 0 в знаменателе.См. Приведенное ниже уравнение.
Наклон — это, по сути, изменение высоты при изменении горизонтального расстояния, и его часто называют «подъем через пробег». Он находит применение в градиентах в географии, а также в гражданском строительстве, например, в строительстве дорог. В случае дороги «подъем» — это изменение высоты, а «пробег» — это разница в расстоянии между двумя фиксированными точками, если расстояние для измерения недостаточно велико, чтобы кривизна земли была рассматривается как фактор.Математически наклон представлен как:
В приведенном выше уравнении y ₂ — y ₁ = Δy или вертикальное изменение, а x ₂ — x ₁ = Δx или горизонтальное изменение, как показано на представленном графике. Также видно, что Δx и Δy — это отрезки прямых, которые образуют прямоугольный треугольник с гипотенузой d , причем d — это расстояние между точками (x ₁, y ₁) и (x ₂, y ₂) .Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d , используя теорему Пифагора. Обратитесь к калькулятору треугольника для получения более подробной информации о теореме Пифагора, а также о том, как рассчитать угол наклона θ , указанный в калькуляторе выше. Кратко:
d = √ (x ₂ — x ₁) ² + (y ₂ — y ₁) ²
Приведенное выше уравнение является теоремой Пифагора в своем корне, где гипотенуза d уже решена, а две другие стороны треугольника определяются вычитанием двух значений x и y , заданных двумя точками. .Учитывая две точки, можно найти θ , используя следующее уравнение:
м = загар (θ)
По точкам (3,4) и (6,8) найдите наклон прямой, расстояние между двумя точками и угол наклона:
d = √ (6-3) ² + (8-4) ² = 5
Хотя это выходит за рамки данного калькулятора, помимо его основного линейного использования, концепция наклона важна в дифференциальном исчислении. Для нелинейных функций скорость изменения кривой меняется, а производная функции в данной точке — это скорость изменения функции, представленная наклоном линии, касательной к кривой в этой точке.
, наклон 1/6, пересечение по оси x при -1
у +1 х + 2 ч. -1 2 13 -4 -5 -6 -7 Отметьте все утверждения, которые верны. O A. Все действительные числа находятся в диапазоне этой функции. Б. Область для … эта функция — набор (-5). C. Область значений этой функции — действительные числа. D. Диапазон для этой функции установлен {-5). E. Этот график не является функцией, потому что значение y одинаково для каждое значение x.
Решите для x: 3 • x • 5 = 5 • x • 3
Какое уравнение представляет собой прямая, параллельная y = 3x-8 и проходящая через точку (4, -5)
Аден хочет получить подписку на онлайн-библиотеку.Есть два варианта подписки, в одном из которых взимается плата. фиксированная годовая плата в размере 96 долларов и … другой, который берет 3 доллара за книгу, которую он берет в долг. Вот график, который показывает систему уравнений для этого сценария, где — количество книг Адена. заимствует, а y — общая стоимость подписки. Что представляет собой S?
Какое из этих выражений эквивалентно log (46)? О. А. журнал (6) — журнал (4) Б. журнал (6) + журнал (4) C. 6. журнал (4) D. журнал (6). журнал (4)
У Мары есть единичные кубы, длина которых составляет 1 или 5 сантиметров.Она использует единичные кубы, чтобы построить прямоугольную призму. В основании призмы всего 1 … 2 куба и призма 5 кубиков в высоту. Каков объем прямоугольной призмы, которую строит Мара?
Густаво убегает на восток на 300 \, \ text {m} 300m300, начальный текст, m, конечный текст, а Эйден убегает более южной линией на 250 \, \ text {m} 250m2. … 50, начальный текст, м, конечный текст. Густаво и Эйден заканчивают 262 \, \ text {m} 262m262, начальный текст, m, конечный текст отдельно, как показано. На сколько градусов от востока Эйден повернул перед тем, как побежать? Не округляйте при расчетах.Округлите окончательный ответ до ближайшей степени.
Как назывался орбитальный телескоп, который помогал исследовать космос, делая такие изображения? (1 балл) О космический телескоп Хаббла O Международный … космический телескоп Космический телескоп Аполлона О космический телескоп Галилео Мне нужна помощь, пожалуйста
1. Напишите уравнение прямой, проходящей через точки (-3, -9) и (5. -9). 2. Напишите уравнение в форме пересечения наклона линии, которая проходит … проходит через точки (-2,10) и (5, -11)
оцените следующее……..
Прямолинейные уравнения: форма пересечения наклона | Purplemath
Purplemath
Прямолинейные уравнения, или «линейные» уравнения, изображаются в виде прямых линий и имеют простые выражения переменных без показателей степени. Если вы видите уравнение только с x и y — в отличие от, скажем, x ² или sqrt ( y ) — тогда вы имеете дело с уравнением прямой линии.
Существуют различные типы «стандартных» форматов прямых линий; конкретный «стандартный» формат, к которому относится ваша книга, может отличаться от формата, используемого в некоторых других книгах. (По иронии судьбы стандартного определения «стандартной формы» не существует.)
MathHelp.com
Различные «стандартные» формы часто унаследованы от нескольких веков назад, когда математики не могли обрабатывать очень сложные уравнения, поэтому они, как правило, зацикливались на простых случаях.В настоящее время вам, вероятно, не нужно слишком беспокоиться о «стандартных» формах; в этом уроке будут рассмотрены только наиболее полезные формы.
Я думаю, что наиболее полезной формой линейных уравнений является форма «наклон-пересечение»:
y = m x + b
Это называется формой пересечения уклона, потому что « м » — это наклон, а « b » дает пересечение y .(Чтобы узнать, как это уравнение используется для построения графиков, посмотрите на наклон и график.)
Мне больше всего нравится форма с пересечением склонов. Он имеет форму « y =», что упрощает подключение для построения графиков или решения текстовых задач. Просто вставьте свое значение x ; уравнение уже решено для y . Кроме того, это единственный формат, который вы можете использовать в своем (в настоящее время обязательном) графическом калькуляторе; у вас должен быть формат « y =» для использования графической утилиты.Но самое лучшее в форме пересечения наклона — это то, что вы можете считать наклон и точку пересечения прямо из уравнения. Это отлично подходит для построения графиков и может быть весьма полезно для текстовых задач.
Партнер
Общие упражнения дадут вам некоторую информацию о линии, и вам нужно будет придумать уравнение линии.Как ты это делаешь? Вы подключаете все, что они вам дают, и решаете все, что вам нужно, например:
Найдите уравнение прямой, имеющей наклон
м = 4 и проходящей через точку (–1, –6).
Хорошо, они дали мне значение наклона; в данном случае м = 4. Кроме того, давая мне точку на линии, они дали мне значение x и значение y для этой линии: x = –1 и y = — 6.
В форме пересечения наклона прямой у меня есть y , m , x и b . Они дали мне значение m, а также значения x и y. Так что единственное, чего у меня пока нет, — это значение b (что дает мне перехват y ). Затем все, что мне нужно сделать, это подключить то, что они дали мне для наклона и x и y от этой конкретной точки, а затем решить для b :
y = m x + b
(–6) = (4) (- 1) + b
–6 = –4 + b
–2 = b
Тогда уравнение линии должно быть « y = 4 x — 2″.
Что, если они не дадут вам уклон?
Найдите уравнение прямой, проходящей через точки (–2, 4) и (1, 2).
Ну, если у меня есть две точки на прямой, я всегда могу найти наклон; вот для чего нужна формула наклона.
Теперь у меня есть наклон и две точки.Я знаю, что могу найти уравнение (сначала решив « b »), если у меня есть точка и наклон; это то, что я сделал в предыдущем примере. Здесь у меня есть , две точки , которые я использовал, чтобы найти наклон. Теперь мне нужно выбрать , одну из точек (не имеет значения, какая из них) и использовать ее для решения для b .
Используя точку (–2, 4), я получаю:
y = m x + b
4 = (- ²/₃) (- 2) + b
4 = ⁴/₃ + b
4-⁴/₃ = b
¹²/₃—⁴/₃ = b
b = ⁸/₃
…so y = (- ²/₃) x + ⁸/₃.
С другой стороны, если я использую точку (1, 2), я получаю:
y = m x + b
2 = (- ²/₃) (1) + b
2 = — ²/₃ + b
2 + ²/₃ = b
⁶/₃ + ²/₃ = b
b = ⁸/₃
Так что неважно, какую точку я выберу.В любом случае ответ один и тот же:
Как видите, если у вас есть наклон, не имеет значения, какую точку вы используете, чтобы найти линейное уравнение. В любом случае ответ будет одинаковым.
URL: https://www.purplemath.com/modules/strtlneq.htm

Промежуточная алгебра
Урок 15: Наклон прямой
WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня
Цели обучения
По завершении этого руководства вы сможете:
Найдите наклон по графику, двум точкам или уравнению.
Напишите линейное уравнение в форме наклона / точки пересечения.
Определите, параллельны ли две прямые, перпендикулярны или нет.
Введение

В этом руководстве мы немного углубимся в линейную уравнения. Мы будем смотреть на наклон линии. Мы также рассмотрим в соотношение между наклонами параллельных линий, а также перпендикуляр линий. Посмотрим, что можно делать со склонами.
Учебник

Наклон линии измеряет крутизну линия.
Большинство из вас, вероятно, знакомы с ассоциацией наклона с «подъемом» перебег ».
Повышение означает, на сколько единиц вы продвинетесь или вниз от точки к точка. На графике это будет изменение на значений на .
Бег означает, как далеко вы двигаетесь влево или вправо от точки к точке. На графике это будет означать изменение на x значений .

Вот несколько иллюстраций, которые помогут вам в этом определение:
Положительный наклон:
Обратите внимание, что когда линия имеет положительный наклон, она идет вверх слева направо.

Отрицательный наклон:
Обратите внимание, что когда линия имеет отрицательный наклон, она идет вниз слева направо.

Нулевой наклон:
наклон = 0
Обратите внимание, что когда линия горизонтальна, наклон равен 0.

Неопределенный уклон:
наклон = не определено
Обратите внимание, что, когда линия вертикальная, наклон неопределенный.

Формула наклона с двумя точками
С учетом двух очков и

Нижние индексы просто указывают, что это два разные точки. Неважно, какой из них вы называете точкой 1, а какой — точка 2 при условии, что вы последовательны в решении этой проблемы.
Обратите внимание, что мы используем букву м для обозначения склон.
Пример 1 : Найдите наклон прямой, проходящей через (-5, 2) и (4, -7).

* Вставьте значения x и y в формулу наклона
* Упростить

Будьте осторожны когда один из ваши значения отрицательны, и вы должны вычесть их, как мы это делали в строке 2. 4 — (-5) не то же самое, что 4-5.
Уклон линии -1.

Пример 2 : Найдите наклон прямой, проходящей через через (1, 1) и (5, 1).

* Вставьте значения x и y в формулу наклона
* Упростить

0 в числителе — это нормально.Помнить что 0 разделено на любое ненулевое число равно 0.
Наклон прямой 0.

Пример 3 : Найдите наклон прямой, проходящей через (3, 4) и (3, 6).

* Вставьте значения x и y в формулу наклона
* Упростить

Поскольку у нас не было изменений в значениях x , знаменатель нашего наклона стал 0.Это означает, что мы имеют неопределенный наклон . Если бы вы изобразили линию, Это будет вертикальной линией, как показано выше.
Наклон линии не определен.

Уравнение наклона / пересечения Строка

Если ваше линейное уравнение записано в этой форме, м представляет наклон, а b представляет y — перехват.
Эта форма может пригодиться, если вам нужно найти уклон строка дана уравнение.

Функциональное обозначение
Уравнение наклона / пересечения прямой

м все еще представляет собой уклон и b по-прежнему представляет собой перехват y .

Пример 4 : Найдите наклон и точку пересечения и линии.

Как упоминалось выше, если уравнение находится в наклоне / пересечении форма , мы легко можем увидеть, какой наклон и y — перехват находятся.
Пойдем дальше и выйдем на склон / перехват форма первая:

* Под. 3x и прибавить 6 к обеим сторонам
* Инверсная по отношению к мульт. на 3 — div. по 3
* Записано в форме наклона / пересечения

Выровняйте форму по полученному уравнению, можете ли вы посмотри какой наклон а y-перехват есть?
В таком виде уклон м, , какой число перед x.В нашей проблеме это должно быть -1.
В этом виде y -перехват равно b , что является константой. В нашей проблеме это было бы быть 2.
Ответ: наклон равен -1, а точка пересечения оси Y равна 2.

Пример 5 : Найдите наклон и точку пересечения y линии.

Этот пример написан в функциональной нотации, но все еще линейный. Как показано выше, вы все еще можете считывать данные вне наклона и пересекать это способ написания.
В этом примере это уже записано в форма наклона / пересечения, так что нам не нужно возиться с этим.Мы можем перейти к бизнес и ответим на наш вопрос, что такое наклон и y — перехват.

* Записывается в форме наклона / пересечения

Выровняйте форму по полученному уравнению, можете ли вы посмотри какой наклон а y-перехват есть?
В таком виде уклон м, , какой число перед x.В нашей проблеме это должно быть 2.
В этом виде y -перехват равно b , что является константой. В нашей проблеме это было бы быть -1.
Ответ: наклон равен 2, а точка пересечения оси Y равна -1.

Пример 6 : Найдите наклон и точку пересечения и строки x = 5.

Так как это особый тип линейного уравнения, не может быть написано в форме наклона / пересечения я покажу вам, что происходит, а затем давайте посмотрим, сможем ли мы вычислить наклон и y — перехват.
График будет выглядеть так:

Сначала поговорим о наклоне.Обратите внимание, что все значения x на этом графике — 5. Это означает изменение x , что является знаменателем формулы наклона, будет 5 — 5 = 0. Ну, вы знаете, что иметь 0 в знаменателе — это большое нет, нет. Это означает, что наклон не определен. Как показано выше, всякий раз, когда ты иметь вертикальную линию, ваш наклон не определен .
Теперь давайте посмотрим на интервал y . Глядя на график, вы можете видеть, что он никогда не пересекает ось y , поэтому нет y -перехват или. Другой способ взглянуть на это — значение x . должно быть 0 при поиске перехвата y и в этой задаче x всегда равно 5.
Итак, несмотря на все наши усилия по решению этой проблемы, мы обнаружили, что наклон undefined и перехват y не существовать.

Пример 7 : Найдите наклон и точку пересечения y строки y = -2.

Так как это особый тип линейного уравнения, не может быть написано в форме наклона / пересечения я покажу вам, что происходит, а затем давайте посмотрим, сможем ли мы вычислить наклон и y — перехват.
График будет выглядеть так:

Сначала поговорим о наклоне. Обратите внимание, как все из y значений на этом графике равны -2. Это означает изменение на , числитель формулы наклона будет -2 — (-2) = 0.Имея 0 в числителе и ненулевое число в знаменателе означает только одна вещь. Наклон равен 0.
Теперь давайте посмотрим на интервал y . Глядя на график, вы можете видеть, что он пересекает ось y . в (0, -2). Таким образом, точка пересечения по оси Y равна (0, -2).
Наклон 0 и пересечение y является -2.

Параллельные линии и их уклоны

Другими словами, наклон параллельных прямых одинаковый.
Обратите внимание, что две строки параллельно, если есть склоны равны и имеют разные y -перехватывания.

Перпендикулярные линии и их Склоны

Другими словами, перпендикулярно уклоны отрицательные взаимны друг с другом.

Пример 8 : Определите, параллельны ли линии, перпендикуляр, или ни то, ни другое. а также .

Чтобы эти линии были параллельны их наклонам хотел бы быть равными и быть перпендикулярными, они должны быть отрицательными взаимные друг друга.
Итак, давайте выясним, какие бывают склоны. Поскольку уравнения уже в форме наклона / пересечения, мы можем посмотреть на них и увидеть отношение между склонами. Что вы думаете? Склон первое уравнение 7 и наклон второго уравнения является 7 .
Так как два уклона равны и их y -пересекаются различны, две линии должны быть параллельны.

Пример 9 : Определите, параллельны ли линии, перпендикуляр, или ни то, ни другое. а также .

Опять же, уравнения уже находятся в наклоне / пересечении форма, так что давайте идите прямо к поиску откоса.Что ты нашел?
Я обнаружил, что наклон первого уравнения равен 4 и наклон второго уравнения равен -1/4. Так что это иметь в виду?
Поскольку два наклона являются отрицательными, обратными каждому другой, две линии будут перпендикулярны друг другу.

Пример 10 : Определите, параллельны ли линии, перпендикуляр, или ни то, ни другое.а также .

Запись первого уравнения в наклон / точку пересечения форму получаем:

* Инверсия сложения 10 x — sub. 10 x
* Записано в форме наклона / пересечения

Запись второго уравнения в наклон / точку пересечения форму получаем:

* Инверсия сложения 4 x — sub.4 x
* Инверсная по отношению к мульт. на 2 — это div. по 2
* Записано в форме наклона / пересечения

Чтобы эти линии были параллельны их наклонам хотел бы быть равными и быть перпендикулярными, они должны быть отрицательными взаимные друг друга.Итак, давайте выясним, какие бывают уклоны. С уравнения теперь в форме наклона / пересечения, мы можем посмотреть на них и увидеть взаимосвязь между наклонами. Что ты считать?
Наклон первого уравнения равен -10 и наклон второе уравнение -2.
Так как два уклона не равны и не равны отрицательные обратные друг друга, то ответ будет ни то, ни другое.

Практические задачи
Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Математика работает так же, как что-нибудь иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшим спортсменам и музыкантам помогали на протяжении всего пути. практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики.
Чтобы получить от них максимальную отдачу, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, щелкнув ссылку для ответ / обсуждение для этой проблемы .По ссылке вы найдете ответ а также любые шаги, которые позволили найти этот ответ.
Практика Задача 1a — 1b: Найдите наклон прямой что проходит через данные баллы.
Практика Задачи 2a — 2c: Найдите наклон и пересечение y линии.
Практика Задачи 3a — 3b: Определите, параллельны ли линии, перпендикуляр, или ни то, ни другое.
Практика Задача 4a: Определите наклон линии.

Нужна дополнительная помощь по этим темам?

Последняя редакция 3 июля 2011 г. Ким Сьюард.
Авторские права на все содержание (C) 2001 — 2011, WTAMU и Kim Seward.
Related Articles
Дом 12 на 8 одноэтажный: готовые и типовые. Каталог содержит планировки, планы и чертежи
alexxlab 12.02.198607.01.2022
Первая помощь отравление окисью углерода: Первая помощь при отравлении окисью углерода: правила оказания – Отравление окисью углерода: признаки, первая помощь, лечение
alexxlab 03.12.202006.02.2020
Печь отопительная в гараж: Небольшие печи для гаража и бытовок длительного горения на дровах
alexxlab 30.06.197317.08.2021
Навигация по записям
Previous post: Обшивка деревянной двери: Обивка деревянных входных дверей
Next post: План дома 8 на 6 двухэтажный: планировки, проекты с мансардой одно и двухэтажных домов
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Инструменты
Облицовка
Отделка
Ремонт
Своими руками
Советы
Стены
Разное
Мини гостиница «Отель А»
© Гостиница «Отель А» Саратов, 2024